The Frustrating Paradox Holding Back Smaller AI Models
(And the Breakthrough That Solves It)
Deep learning powers everything from medical imaging to self-driving cars. But there’s a dirty secret: these models are monstrously huge. Deploying them on phones, embedded devices, or real-time systems often feels impossible. That’s why knowledge distillation (KD) became essential:
- The Promise: Train a compact “student” model (e.g., MobileNet) to mimic a powerful “teacher” (e.g., ResNet-152)
- The Standard: Blend cross-entropy loss (for correct labels) with KL divergence loss (to match teacher probabilities)
- The Paradox: Bigger teachers should help students… but often degrade performance due to capacity mismatch!
Researchers tried fixes—teacher assistants, selective distillation, auxiliary modules. They added complexity, not solutions. Even state-of-the-art methods like DIST (2022) still needed manual balancing between cross-entropy and distillation terms.
Figure 1(a) Proof: Reducing cross-entropy weight (α) boosts accuracy temporarily… but dropping it entirely crashes performance. Tuning α is fragile and dataset-dependent.
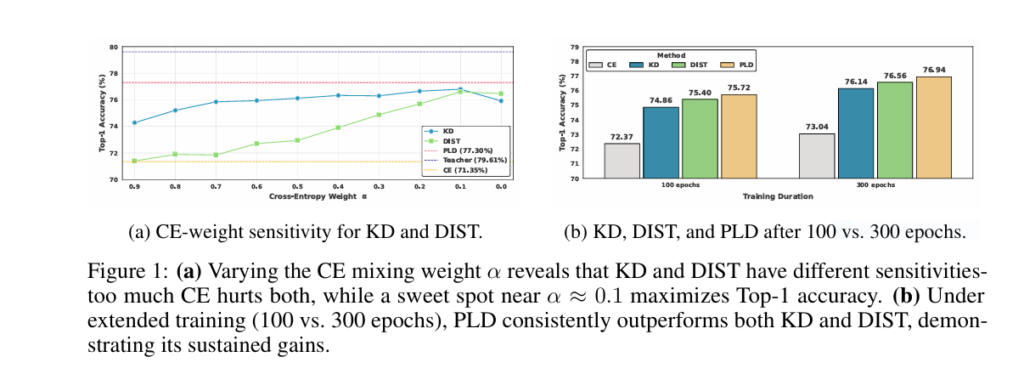
Engineers wasted months tuning α, τ, β, γ… only to see tiny (±0.1%) gains evaporate with new data. The core problem remained:
“How do you transfer a teacher’s wisdom to a smaller student WITHOUT delicate balancing acts or performance cliffs?”
PLD: Rewriting Knowledge Distillation with Choice Theory & Rankings
(No More Manual Weight Tuning)
Researchers from Peking University cracked the code by rethinking distillation fundamentals. Their solution, Plackett-Luce Distillation (PLD), throws out probability matching. Instead, it leverages:
- Choice Theory: Treats teacher logits as “worth” scores (Luce’s Axiom)
- Plackett-Luce Model: Generates rankings where classes are selected sequentially based on worth
- Teacher-Optimal Permutation (π*): A single ranking target:
- Ground-truth label FIRST
- Remaining classes ordered by descending teacher confidence
This eliminates probability matching entirely. PLD enforces π* via a novel loss weighted by the teacher’s own confidence at each step:
ℒₚₗ𝒹(𝑠, 𝑡; 𝑦) = ∑ₖ₌₁ᶜ 𝑞ₜ{πₖ*} ⋅ [ -𝑠{πₖ*} + log ∑{ℓ=𝑘}ᶜ exp(𝑠{πℓ*}) ]
Why This Works:
| Traditional KD/DIST | PLD (Our Method) |
|---|---|
| Tunes α balancing CE + Distill | Single unified loss |
| Matches probabilities (KL/correlation) | Matches structured rankings |
| Sensitive to teacher overfitting | Confidence-weighted steps |
| Non-convex optimization | Convex & translation-invariant |
Smashing Benchmarks: +1.09% Accuracy Gains Validated
*(ResNet-50 → ViT Results Inside)*
Rigorous ImageNet-1K tests proved PLD’s dominance:
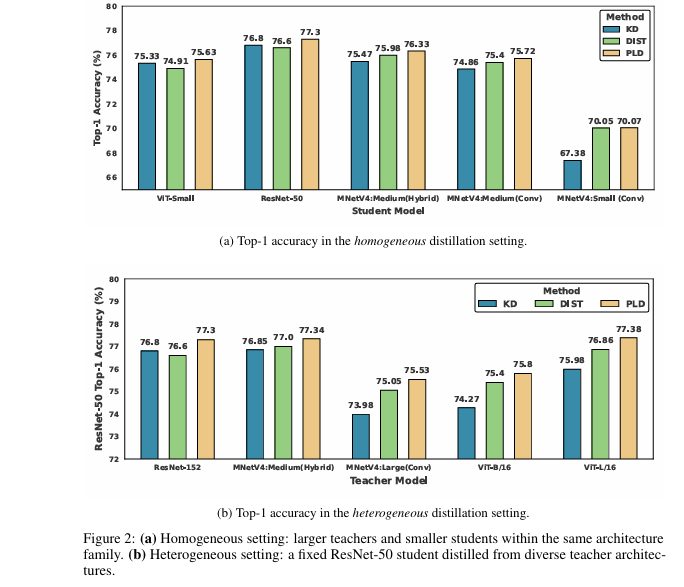
Homogeneous Settings (Same Architecture Family)
Table: PLD Accuracy Gains vs. DIST & KD
| Teacher → Student | DIST Top-1 | PLD Top-1 | Δ vs. DIST | KD Top-1 | Δ vs. KD |
|---|---|---|---|---|---|
| ViT-Large → ViT-Small | 74.91% | 75.63% | +0.72% | 75.33% | +0.30% |
| ResNet-152 → ResNet-50 | 76.60% | 77.30% | +0.70% | 76.80% | +0.50% |
| MobileNet-L → MobileNet-S | 70.05% | 70.07% | +0.02% | 67.38% | +2.69% |
| AVERAGE GAIN | +0.42% | +1.04% |
Smaller students saw massive jumps (up to +2.69%). PLD thrives under capacity mismatch.
Heterogeneous Settings (Cross-Architecture)
*Table: ResNet-50 Student w/ Diverse Teachers*
| Teacher Model | DIST Top-1 | PLD Top-1 | Δ vs. DIST | KD Top-1 | Δ vs. KD |
|---|---|---|---|---|---|
| ResNet-152 | 76.60% | 77.30% | +0.70% | 76.80% | +0.50% |
| ViT-Large/16 | 76.86% | 77.38% | +0.52% | 75.98% | +1.40% |
| MobileNetV4-Hybrid | 77.00% | 77.34% | +0.34% | 76.85% | +0.49% |
| AVERAGE GAIN | +0.48% | +1.09% |
Critical Finding: PLD’s gains grow as teachers get larger—solving the core paradox.
Why PLD Works: The Science of Structured Rankings
(Beyond Marginal Probabilities)
Traditional KD and DIST focus on matching probabilities:
- KD: Minimizes KL divergence (marginal distributions)
- DIST: Preserves inter/intra-class correlations
PLD’s breakthrough: It transfers the teacher’s preference structure.
- Cross-Entropy is Incomplete: Only enforces “correct class #1”. Ignores ordering of runners-up.
- Full Rankings Matter: Knowing class B > C > D if A is wrong improves decision boundaries.
- Teacher Confidence as Weight: Steps where teacher is certain (high softmax) get prioritized.
Technical Advantages:
✅ Convex Loss: Guarantees efficient optimization (Appendix A)
✅ Translation-Invariant: Adding constants to logits doesn’t change gradients
✅ Subsumes CE/ListMLE: Special cases with specific weights (αₖ)
Figure 3(c) Proof: PLD’s loss landscape is smoother and better-centered than DIST or KD.
Implementing PLD: 4-Step Code Guide & Best Practices
(PyTorch Snippet Included)
Step 1: Generate Teacher-Optimal Permutation (π*)
def create_adjusted_ranking(teacher_logits, true_labels):
# Sort teacher logits ASCENDING (low confidence first)
_, sorted_idx = torch.sort(teacher_logits, dim=-1, descending=False)
# Mask out true label from sorted list
mask = sorted_idx != true_labels.unsqueeze(-1)
# Combine: [low-confidence classes, ..., true_label]
return torch.cat([sorted_idx[mask], true_labels.unsqueeze(-1)], dim=-1)
Step 2: Gather Student/Teacher Logits via π*
ranking = create_adjusted_ranking(teacher_logits, labels) s_perm = torch.gather(student_logits, -1, ranking) # Student logits reordered t_perm = torch.gather(teacher_logits, -1, ranking) # Teacher logits reordered
Step 3: Compute Weighted PL Likelihood
log_cumsum = torch.logcumsumexp(s_perm, dim=-1) per_pos_loss = log_cumsum - s_perm teacher_probs = F.softmax(t_perm, dim=-1) # αₖ weights loss = (per_pos_loss * teacher_probs).sum(dim=-1).mean()
Best Practices:
- Temperature τₜ=1.0: Default works best (Table 2)
- No Logit Standardization: Hurts PLD (Table 8)
- Optimizers: Lamb > AdamW > AdaBelief (Table 7)
- Extended Training: Gains persist (+1.22% after 300 epochs)
If you’re Interested in semi-supervised learning with Knowledge Distillation model, you may also find this article helpful:Unlock 106x Faster MD Simulations: The Knowledge Distillation Breakthrough Accelerating Materials Discovery
Limitations & The Future of Ranking-Based Knowledge Distillation
PLD isn’t a silver bullet:
⚠️ Requires aligned class vocabularies (no incremental learning)
⚠️ O(ClogC) cost per sample vs. O(C) for KD (matters for 10K+ classes)
⚠️ Diminishes if teacher is uncalibrated (near-uniform probabilities)
Future Frontiers:
➡️ Adaptive Weighting: Modulate αₖ based on sample difficulty
➡️ Beyond Classification: Reinforcement learning, sequence modeling
➡️ Hardware-Aware Compression: Couple PLD with quantization/pruning
Conclusion: Stop Tuning, Start Ranking
Knowledge distillation hit a wall—bigger teachers couldn’t teach smaller students effectively. PLD breaks that wall by reframing distillation as a structured ranking problem.
Proven Results:
🔹 +0.42% avg. gain over DIST
🔹 +1.09% avg. gain over vanilla KD
🔹 Simpler implementation, no α/β/γ tuning
Call to Action:
- Researchers: Explore PLD for speech/NLP tasks (Paper Link)
- Engineers: Replace KL loss with PLD in your pipeline using our below Code
- Leaders: Audit model compression ROI—PLD adds accuracy without inference costs
“PLD isn’t just incremental—it’s the first distillation method that leverages the full ranking structure of teacher knowledge. Tuning weights is officially obsolete.” – Kaigui Bian, Lead Author
Complete Implementation of Plackett-Luce Distillation (PLD).
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
import timm
class PLDLoss(nn.Module):
"""
Plackett-Luce Distillation Loss (PLD)
Implements the list-wise knowledge distillation method from:
"PLD: A Choice-Theoretic List-Wise Knowledge Distillation" (https://arxiv.org/abs/2506.12542v2)
Args:
temperature (float): Softmax temperature for teacher confidence weighting
"""
def __init__(self, temperature=1.0):
super().__init__()
self.temperature = temperature
def forward(self, student_logits, teacher_logits, labels):
"""
Compute PLD loss
Args:
student_logits (torch.Tensor): Student model logits [batch_size, num_classes]
teacher_logits (torch.Tensor): Teacher model logits [batch_size, num_classes]
labels (torch.Tensor): Ground truth labels [batch_size]
Returns:
torch.Tensor: PLD loss value
"""
batch_size, num_classes = student_logits.shape
# Step 1: Create teacher-optimal permutation π*
# [true_label, remaining classes sorted by teacher confidence (descending)]
permutations = torch.zeros_like(teacher_logits, dtype=torch.long)
# Start permutation with true label
permutations[:, 0] = labels
# Create mask to exclude true labels
mask = torch.ones_like(teacher_logits, dtype=torch.bool)
mask[torch.arange(batch_size), labels] = False
# Sort remaining classes by teacher confidence (descending)
_, sorted_indices = torch.sort(teacher_logits, descending=True)
# Fill permutation with remaining classes
for i in range(batch_size):
remaining = sorted_indices[i][mask[i, sorted_indices[i]]]
permutations[i, 1:1+len(remaining)] = remaining[:num_classes-1]
# Step 2: Gather permuted logits
sperm = torch.gather(student_logits, 1, permutations) # Student in π* order
tperm = torch.gather(teacher_logits, 1, permutations) # Teacher in π* order
# Step 3: Compute tail sums for student logits
rev = torch.flip(sperm, dims=[-1])
rev_cumsum = torch.logcumsumexp(rev, dim=-1)
tail_logsumexp = torch.flip(rev_cumsum, dims=[-1])
# Step 4: Compute position-wise loss
per_pos_loss = tail_logsumexp - sperm
# Step 5: Compute teacher confidence weights
teacher_probs = F.softmax(tperm / self.temperature, dim=-1)
# Step 6: Apply confidence weighting and average
loss_per_sample = torch.sum(teacher_probs * per_pos_loss, dim=-1)
return loss_per_sample.mean()
class PLDKnowledgeDistillation:
"""
End-to-end PLD Knowledge Distillation Framework
Args:
teacher_model (nn.Module): Pretrained teacher model
student_model (nn.Module): Student model to be trained
temperature (float): Temperature for PLD loss
lr (float): Learning rate
device (str): Device for training ('cuda' or 'cpu')
"""
def __init__(self, teacher_model, student_model, temperature=1.0, lr=0.01, device='cuda'):
self.teacher = teacher_model.to(device)
self.student = student_model.to(device)
self.device = device
self.criterion = PLDLoss(temperature)
self.optimizer = torch.optim.AdamW(self.student.parameters(), lr=lr)
self.teacher.eval() # Teacher in evaluation mode
def train_step(self, images, labels):
"""Single training step"""
images, labels = images.to(self.device), labels.to(self.device)
with torch.no_grad():
teacher_logits = self.teacher(images)
student_logits = self.student(images)
# Compute PLD loss
loss = self.criterion(student_logits, teacher_logits, labels)
# Optimize student
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
return loss.item()
def validate(self, test_loader):
"""Evaluate student model"""
self.student.eval()
correct, total = 0, 0
with torch.no_grad():
for images, labels in test_loader:
images, labels = images.to(self.device), labels.to(self.device)
outputs = self.student(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
self.student.train()
return correct / total
def fit(self, train_loader, epochs, test_loader=None):
"""Full training loop"""
results = {'train_loss': [], 'val_acc': []}
for epoch in range(epochs):
epoch_loss = 0.0
for i, (images, labels) in enumerate(train_loader):
loss = self.train_step(images, labels)
epoch_loss += loss
if (i+1) % 50 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Step [{i+1}/{len(train_loader)}], Loss: {loss:.4f}')
avg_loss = epoch_loss / len(train_loader)
results['train_loss'].append(avg_loss)
if test_loader:
val_acc = self.validate(test_loader)
results['val_acc'].append(val_acc)
print(f'Epoch [{epoch+1}/{epochs}], Loss: {avg_loss:.4f}, Val Acc: {val_acc:.4f}')
else:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {avg_loss:.4f}')
return results
# Example Usage
if __name__ == "__main__":
# Configuration
device = 'cuda' if torch.cuda.is_available() else 'cpu'
batch_size = 128
epochs = 10
temperature = 1.0
learning_rate = 0.001
# Load dataset (example with CIFAR-10)
transform = transforms.Compose([
transforms.Resize((224, 224)),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
train_dataset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
test_dataset = datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
# Initialize models (example with ResNets)
teacher = timm.create_model('resnet152', pretrained=True, num_classes=10)
student = timm.create_model('resnet50', pretrained=True, num_classes=10)
# Initialize PLD framework
distiller = PLDKnowledgeDistillation(
teacher_model=teacher,
student_model=student,
temperature=temperature,
lr=learning_rate,
device=device
)
# Train and evaluate
results = distiller.fit(train_loader, epochs, test_loader)
# Save distilled student
torch.save(student.state_dict(), 'distilled_student.pth')
Pingback: 7 Incredible Upsides and Downsides of Layered Self‑Supervised Knowledge Distillation (LSSKD) for Edge AI - aitrendblend.com