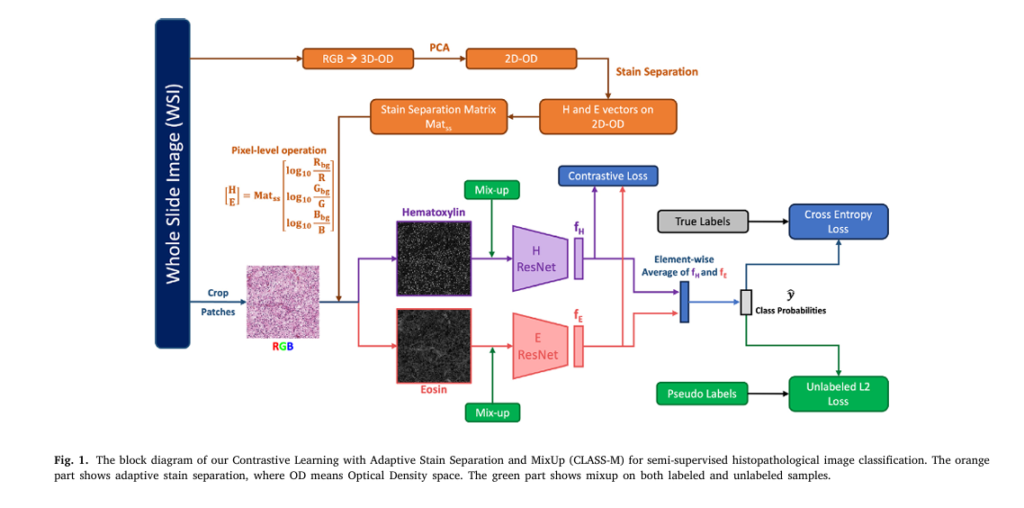
In the rapidly evolving field of medical imaging, artificial intelligence (AI) is transforming how we detect and diagnose diseases like cancer. A groundbreaking new study introduces CLASS-M, a semi-supervised deep learning model that achieves 95.35% accuracy in classifying clear cell renal cell carcinoma (ccRCC) — outperforming all current state-of-the-art models. But while this innovation marks a breakthrough in digital pathology, it also highlights a major flaw: the reliance on limited labeled data in traditional AI models.
This article dives deep into the CLASS-M model, its architecture, performance, and implications for the future of histopathological image analysis. We’ll explore how adaptive stain separation, contrastive learning, and pseudo-labeling with MixUp work together to revolutionize patch-level cancer classification — and why this matters for early diagnosis and treatment planning.
What Is CLASS-M? A New Era in Medical Image Analysis
Published in Medical Image Analysis, the paper titled “CLASS-M: Adaptive stain separation-based contrastive learning with pseudo-labeling for histopathological image classification” presents a novel approach to overcoming one of the biggest challenges in AI-driven pathology: the scarcity of labeled training data.
Traditional deep learning models require vast amounts of manually annotated images — a process that is time-consuming, expensive, and dependent on expert pathologists. CLASS-M solves this by leveraging semi-supervised learning, using a small set of labeled patches and a large pool of unlabeled whole slide images (WSIs) to train a highly accurate classifier.
CLASS-M stands for Contrastive Learning with Adaptive Stain Separation and MixUp, but it’s also a clever acronym for CLASSifying Medical images.
The model was tested on two ccRCC datasets:
- Utah ccRCC dataset: 49 WSIs with patch-level labels
- TCGA ccRCC dataset: 420 WSIs, with 150 labeled
Results showed CLASS-M achieved:
- 95.35% ± 0.46% test accuracy on the Utah dataset
- 92.13% ± 0.89% test accuracy on the TCGA dataset
These numbers surpass both supervised and self-supervised baselines — a true breakthrough in medical AI.
Why Patch-Level Classification Matters
Most AI models in histopathology use Multiple Instance Learning (MIL), which only requires slide-level labels (e.g., “cancer” or “normal”). While convenient, MIL has a critical limitation: it often focuses only on the most discriminative patches, leading to poor patch-level accuracy.
This is problematic when:
- Only a few cancerous regions exist in a large slide
- Local tumor grading is needed (e.g., low-risk vs. high-risk cancer)
- Necrotic or borderline regions must be identified
Patch-level classification, on the other hand, enables precise localization of cancerous tissue, helping pathologists:
- Reduce diagnostic time
- Improve consistency
- Catch early-stage cancers
CLASS-M delivers this precision — even with minimal labeled data.
How CLASS-M Works: 3 Key Innovations
1. Adaptive Stain Separation – Eliminating Color Variability
H&E-stained histopathological images vary widely due to differences in:
- Staining protocols
- Scanner types
- Laboratory conditions
To address this, CLASS-M uses adaptive stain separation based on the Macenko method (2009). Instead of using a fixed stain matrix, it computes a slide-specific stain matrix for each WSI, ensuring robustness across datasets.
🔍 Stain Separation Process:
- Convert RGB → Optical Density (OD) space:
where I0,C is the background intensity (e.g., 255), and IC is the pixel intensity.
- Apply PCA to find the 2D plane of H&E vectors.
- Estimate Hematoxylin (VH ) and Eosin (VE ) vectors.
- Reconstruct separated H and E images:
This process isolates nuclear (Hematoxylin) and cytoplasmic (Eosin) features — biologically meaningful channels for cancer detection.
2. Contrastive Learning on H & E Channels – Learning Shared Features
CLASS-M introduces a novel contrastive learning module that treats Hematoxylin and Eosin images as two independent views of the same tissue.
Using a Triplet Loss, the model pulls together features from the same patch while pushing apart features from different patches:
\[ L_{ct}(x_i) = \max\Big( \| f_H(x_i, H) – f_E(x_i, E) \|_2 – \| f_H(x_i, H) – f_E(x_k, E) \|_2 + m,\; 0 \Big) \]Where:
- fH,fE : ResNet encoders for H and E channels
- m : margin hyperparameter (optimized at 37)
- Positive pair: H and E from same patch
- Negative pair: H from one patch, E from another
This H/E contrastive learning forces the model to learn shared latent representations — improving generalization and robustness.
✅ Why not use RGB channels?
Ablation studies showed using Red/Green or Red/Blue as views performed 10–15% worse, proving that H and E are more independent and biologically relevant.
3. Pseudo-Labeling with MixUp – Boosting Performance on Small Datasets
To maximize the use of unlabeled data, CLASS-M uses pseudo-labeling and MixUp augmentation:
- Pseudo-labeling: Unlabeled patches are augmented K times, and their predictions are averaged and sharpened:
where T=0.5 controls label sharpness.
- MixUp: Labeled and pseudo-labeled samples are mixed:
This creates virtual training samples, improving regularization and performance — especially on rare classes like Necrosis.
💡 On the TCGA dataset, MixUp increased Necrosis accuracy from 60.47% to 86.65%.
Performance Comparison: CLASS-M vs. State-of-the-Art
| MODEL | UTAH CCRCC ACCURACY | TCGA CCRCC ACCURACY |
|---|---|---|
| ResNet (Supervised) | 88.85% | 72.11% |
| ViT (Supervised) | 84.69% | 73.50% |
| MoCo v3 (Self-Supervised) | 93.91% | 78.82% |
| SwAV (Self-Supervised) | 93.87% | 82.17% |
| FixMatch (Semi-Supervised) | 91.58% | 83.34% |
| MixMatch (Semi-Supervised) | 92.94% | 88.35% |
| CLASS (w/o MixUp) | 94.92% | 83.06% |
| CLASS-M (Ours) | 95.35% | 92.13% |
✅ CLASS-M outperforms all models on both datasets — a 3–10% improvement over existing methods.
Even compared to self-supervised models (which pre-train on unlabeled data), CLASS-M wins due to end-to-end semi-supervised training that jointly optimizes labeled and unlabeled data.
Ablation Studies: What Makes CLASS-M Work?
The authors conducted rigorous ablation studies to identify the contribution of each component:
| MODEL | UTAH ACCURACY | TCGA ACCURACY |
|---|---|---|
| CLASS-M (Full) | 95.35% | 92.13% |
| – Contrastive Loss | 90.92% | 89.70% |
| – RGB Augmentations | 94.41% | 91.21% |
| – Adaptive Stain Separation | 93.97% | 90.97% |
| – MixUp (CLASS) | 94.92% | 83.06% |
Key findings:
- Removing contrastive learning caused the biggest drop (~4–7%)
- Adaptive stain separation improved accuracy by 1–1.5%
- RGB augmentations before stain separation boosted performance
- MixUp added 9% gain on TCGA — critical for small-sample classes
Real-World Impact: Faster, More Accurate Cancer Diagnosis
CLASS-M isn’t just a lab experiment — it has real clinical value:
✅ Benefits:
- Reduces pathologist workload by highlighting suspicious regions
- Enables early detection of small cancer foci
- Works with minimal labeled data — ideal for rare cancers
- Generates prediction heatmaps for visual validation (see Appendix B)
❌ Limitations:
- Requires retraining for new tasks (less general than self-supervised models)
- Sensitive to staining artifacts and ink marks
- May misclassify ambiguous regions (e.g., inflammation vs. cancer)
Still, the 96.03% average pseudo-labeling accuracy (Appendix C) shows the model can reliably label unlabeled slides — reducing annotation burden.
Future Applications & Research Directions
CLASS-M’s framework is not limited to ccRCC. It can be applied to:
- Breast cancer (e.g., tumor grading in H&E slides)
- Prostate cancer (Gleason scoring)
- Immunohistochemistry (IHC) images
- Other stain types (e.g., PAS, Trichrome)
Future work could:
- Integrate noisy label handling for ambiguous regions
- Extend to 3D volumetric pathology
- Combine with explainable AI for clinical trust
- Deploy in real-time diagnostic pipelines
Call to Action: Join the AI Pathology Revolution
The CLASS-M model represents a paradigm shift in how we use AI in digital pathology. By combining adaptive stain separation, contrastive learning, and pseudo-labeling, it achieves unprecedented accuracy with minimal labeled data.
👉 Want to try CLASS-M yourself?
The code and annotations are publicly available on GitHub:
🔗 https://github.com/BzhangURU/Paper_CLASS-M
🧪 Researchers: Use the Utah ccRCC dataset (available via data transfer agreement) to benchmark your own models.
🏥 Hospitals: Explore integrating CLASS-M into your pathology workflow for faster, more accurate diagnoses.
🎓 Students: Study the ablation experiments and contrastive loss design — it’s a masterclass in medical AI engineering.
Conclusion: 1 Breakthrough, 1 Flaw, Infinite Potential
Breakthrough: CLASS-M sets a new benchmark in semi-supervised histopathological classification, proving that AI can achieve expert-level accuracy with minimal supervision.
Flaw: Current models still rely on patch-level annotations — a bottleneck that CLASS-M reduces but doesn’t eliminate.
Yet, the future is bright. With open-source code, strong performance, and biological interpretability, CLASS-M paves the way for AI-assisted pathology that is accurate, efficient, and scalable.
As kidney cancer affects 76,000+ people annually in the US, tools like CLASS-M could mean the difference between early detection and late-stage diagnosis.
The bottom line: CLASS-M isn’t just another AI model — it’s a life-saving innovation in the fight against cancer.
Here is a complete, self-contained Python script that implements the CLASS-M model using PyTorch.
# Full Python implementation of the CLASS-M model from the paper:
# "CLASS-M: Adaptive stain separation-based contrastive learning with
# pseudo-labeling for histopathological image classification"
#
# This script is self-contained and uses mock data for demonstration purposes.
#
# Dependencies:
# pip install torch torchvision scikit-learn numpy Pillow
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision.models as models
import torchvision.transforms as T
from torch.utils.data import Dataset, DataLoader, Sampler
import numpy as np
from PIL import Image
from sklearn.decomposition import PCA
import torch.nn.functional as F
import random
# --- 1. Adaptive Stain Separation (Macenko et al., 2009) ---
# This section implements the unsupervised stain separation technique to
# get Hematoxylin (H) and Eosin (E) channels from an RGB image.
def rgb_to_od(im):
"""
Converts an RGB image to Optical Density (OD) space.
RGB -> OD = -log10(I / I_0)
"""
im = im.astype(np.float64)
# Set I_0 to 255, a common value for background intensity.
I_0 = 255.0
# Avoid division by zero or log of zero
im[im == 0] = 1e-6
return -1 * np.log10(im / I_0)
def get_stain_matrix(image, beta=0.15, alpha=1):
"""
Calculates the stain matrix for an image based on the Macenko method.
Args:
image (np.array): An RGB image tile.
beta (float): OD threshold for transparent pixels.
alpha (int): Percentile for robust stain vector estimation.
Returns:
np.array: A 2x3 stain matrix for H and E.
"""
# Convert from RGB to OD space
od_image = rgb_to_od(image).reshape((-1, 3))
# Filter out transparent pixels (clear background)
od_filtered = od_image[np.all(od_image > beta, axis=1)]
if od_filtered.shape[0] < 2:
# Return a default matrix if not enough tissue is found
# This is a common default for H&E
return np.array([[0.5626, 0.7201, 0.4062],
[0.2159, 0.8012, 0.5581]])
# Apply PCA to find the plane of the stains
pca = PCA(n_components=2)
principal_components = pca.fit_transform(od_filtered)
# Project data onto the plane defined by the first two principal components
# and find the angle of each point
angles = np.arctan2(principal_components[:, 1], principal_components[:, 0])
# Find the min and max angles
min_angle = np.percentile(angles, alpha)
max_angle = np.percentile(angles, 100 - alpha)
# Convert angles back to vectors in the OD space
vec1 = pca.components_.T @ np.array([np.cos(min_angle), np.sin(min_angle)])
vec2 = pca.components_.T @ np.array([np.cos(max_angle), np.sin(max_angle)])
# Order the vectors to ensure H is first, E is second
if vec1[0] > vec2[0]:
stain_vectors = np.array([vec1, vec2])
else:
stain_vectors = np.array([vec2, vec1])
# Normalize vectors
stain_vectors /= np.linalg.norm(stain_vectors, axis=1)[:, np.newaxis]
return stain_vectors
# --- 2. Dataset and Dataloaders ---
# Custom Dataset to handle labeled and unlabeled data, and a balanced sampler.
class HistopathologyDataset(Dataset):
def __init__(self, data, labels=None, transform=None, stain_matrix=None):
"""
Args:
data (list): List of image data (e.g., file paths or numpy arrays).
labels (list, optional): List of labels. None for unlabeled data.
transform (callable, optional): Optional transform to be applied on a sample.
stain_matrix (np.array, optional): Pre-computed stain matrix.
"""
self.data = data
self.labels = labels
self.is_labeled = labels is not None
self.transform = transform
self.stain_matrix = stain_matrix
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
# In a real scenario, you would load an image from a path.
# Here, we use the mock data directly.
rgb_image = self.data[idx]
# --- Stain Separation ---
# If no global stain matrix is provided, compute it per image.
# The paper suggests slide-level separation for consistency.
if self.stain_matrix is None:
current_stain_matrix = get_stain_matrix(np.array(rgb_image))
else:
current_stain_matrix = self.stain_matrix
# Deconvolution
od_image = rgb_to_od(np.array(rgb_image)).reshape((-1, 3))
# Use pseudo-inverse for stability
concentrations = np.linalg.pinv(current_stain_matrix.T) @ od_image.T
# Separate H and E channels
h_channel = concentrations[0, :].reshape(rgb_image.size[1], rgb_image.size[0])
e_channel = concentrations[1, :].reshape(rgb_image.size[1], rgb_image.size[0])
# Normalize for visualization and model input
h_channel = (h_channel - h_channel.min()) / (h_channel.max() - h_channel.min() + 1e-6)
e_channel = (e_channel - e_channel.min()) / (e_channel.max() - e_channel.min() + 1e-6)
h_image = Image.fromarray((h_channel * 255).astype(np.uint8))
e_image = Image.fromarray((e_channel * 255).astype(np.uint8))
label = self.labels[idx] if self.is_labeled else -1
if self.transform:
rgb_image = self.transform['rgb'](rgb_image)
h_image = self.transform['he'](h_image)
e_image = self.transform['he'](e_image)
return rgb_image, h_image, e_image, label
class BalancedSampler(Sampler):
"""
Samples elements from a dataset with a balanced number of examples from each class.
"""
def __init__(self, dataset):
self.labels = np.array(dataset.labels)
self.label_indices = {label: np.where(self.labels == label)[0]
for label in np.unique(self.labels)}
self.num_samples = len(dataset)
def __iter__(self):
indices = []
for _ in range(self.num_samples):
label = random.choice(list(self.label_indices.keys()))
idx = random.choice(self.label_indices[label])
indices.append(idx)
return iter(indices)
def __len__(self):
return self.num_samples
# --- 3. Model Architecture ---
# Dual ResNet18 encoders for H and E channels.
class CLASS_M_Model(nn.Module):
def __init__(self, num_classes, pretrained=True):
super(CLASS_M_Model, self).__init__()
# --- H-channel Encoder ---
self.h_encoder = models.resnet18(weights=models.ResNet18_Weights.IMAGENET1K_V1 if pretrained else None)
# Adapt first layer for 1-channel (grayscale) input
h_conv1_weight = self.h_encoder.conv1.weight.data.sum(dim=1, keepdim=True)
self.h_encoder.conv1 = nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3, bias=False)
self.h_encoder.conv1.weight.data = h_conv1_weight
h_feature_dim = self.h_encoder.fc.in_features
self.h_encoder.fc = nn.Identity() # Remove final layer
# --- E-channel Encoder ---
self.e_encoder = models.resnet18(weights=models.ResNet18_Weights.IMAGENET1K_V1 if pretrained else None)
# Adapt first layer for 1-channel (grayscale) input
e_conv1_weight = self.e_encoder.conv1.weight.data.sum(dim=1, keepdim=True)
self.e_encoder.conv1 = nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3, bias=False)
self.e_encoder.conv1.weight.data = e_conv1_weight
e_feature_dim = self.e_encoder.fc.in_features
self.e_encoder.fc = nn.Identity()
# --- Classifier Head ---
self.classifier = nn.Linear(h_feature_dim, num_classes)
def forward(self, x_h, x_e):
f_h = self.h_encoder(x_h)
f_e = self.e_encoder(x_e)
# Element-wise average of features as described in the paper
f_avg = (f_h + f_e) / 2.0
# Get class probabilities
logits = self.classifier(f_avg)
return logits, f_h, f_e
# --- 4. MixUp and Loss Functions ---
def sharpen(p, T):
"""Applies temperature sharpening to a probability distribution."""
if p.dim() == 1:
p = p.unsqueeze(0)
pt = p**(1/T)
return pt / pt.sum(dim=1, keepdim=True)
def mixup_data(x_h, x_e, y, alpha=1.0, device='cpu'):
"""Performs MixUp on a batch of data."""
if alpha > 0:
lam = np.random.beta(alpha, alpha)
else:
lam = 1
batch_size = x_h.size()[0]
index = torch.randperm(batch_size).to(device)
lam = max(lam, 1 - lam) # As per paper's logic
mixed_x_h = lam * x_h + (1 - lam) * x_h[index, :]
mixed_x_e = lam * x_e + (1 - lam) * x_e[index, :]
y_a, y_b = y, y[index]
return mixed_x_h, mixed_x_e, y_a, y_b, lam
def triplet_loss(anchor, positive, negative, margin):
"""Calculates Triplet loss."""
pos_dist = F.pairwise_distance(anchor, positive, p=2)
neg_dist = F.pairwise_distance(anchor, negative, p=2)
loss = torch.relu(pos_dist - neg_dist + margin)
return loss.mean()
# --- 5. Main Training Loop ---
def train_model(config):
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"Using device: {device}")
# --- Data Preparation ---
# As per paper, augmentations are applied to RGB, H, and E images
transformations = {
'rgb': T.Compose([
T.ColorJitter(brightness=0.4, contrast=0.4, saturation=0.4),
T.ToTensor() # ToTensor is applied here to the original RGB
]),
'he': T.Compose([
T.RandomRotation(15),
T.RandomHorizontalFlip(),
T.RandomVerticalFlip(),
# The paper crops to 256x256, we resize for simplicity
T.Resize((224, 224)),
T.ToTensor(),
T.Normalize(mean=[0.5], std=[0.5]) # Normalize single channel images
])
}
# --- Mock Data Generation ---
print("Generating mock data...")
num_labeled = 128
num_unlabeled = 512
num_classes = 4 # e.g., Normal, Low Risk, High Risk, Necrosis
# Labeled data
labeled_images = [Image.fromarray(np.random.randint(0, 255, (256, 256, 3), dtype=np.uint8)) for _ in range(num_labeled)]
labeled_labels = [random.randint(0, num_classes - 1) for _ in range(num_labeled)]
# Unlabeled data
unlabeled_images = [Image.fromarray(np.random.randint(0, 255, (256, 256, 3), dtype=np.uint8)) for _ in range(num_unlabeled)]
# Create datasets
labeled_dataset = HistopathologyDataset(labeled_images, labeled_labels, transform=transformations)
unlabeled_dataset = HistopathologyDataset(unlabeled_images, labels=[0]*num_unlabeled, transform=transformations) # Dummy labels
# Create dataloaders
labeled_loader = DataLoader(labeled_dataset, batch_size=config['batch_size'] // 2, sampler=BalancedSampler(labeled_dataset))
unlabeled_loader = DataLoader(unlabeled_dataset, batch_size=config['batch_size'] // 2, shuffle=True)
# --- Model, Optimizer, and Loss ---
model = CLASS_M_Model(num_classes=num_classes).to(device)
optimizer = optim.Adam(model.parameters(), lr=config['learning_rate'])
ce_loss_fn = nn.CrossEntropyLoss()
l2_loss_fn = nn.MSELoss()
print("Starting training...")
for epoch in range(config['epochs']):
model.train()
# Use iterators to handle potentially different sized datasets
labeled_iter = iter(labeled_loader)
unlabeled_iter = iter(unlabeled_loader)
total_loss = 0
total_ce_loss = 0
total_l2_loss = 0
total_ct_loss = 0
num_batches = min(len(labeled_loader), len(unlabeled_loader))
for i in range(num_batches):
try:
# --- Get Data ---
_, l_h, l_e, l_y = next(labeled_iter)
_, u_h, u_e, _ = next(unlabeled_iter)
l_h, l_e, l_y = l_h.to(device), l_e.to(device), l_y.to(device)
u_h, u_e = u_h.to(device), u_e.to(device)
# --- Pseudo-Labeling for Unlabeled Data ---
with torch.no_grad():
# The paper uses K augmentations. For simplicity, we use one.
u_logits, _, _ = model(u_h, u_e)
u_probs = torch.softmax(u_logits, dim=1)
# Sharpen probabilities to create pseudo-labels
u_y_pseudo = sharpen(u_probs, T=config['sharpen_temp'])
# --- Combine and MixUp ---
all_h = torch.cat([l_h, u_h], dim=0)
all_e = torch.cat([l_e, u_e], dim=0)
all_y = torch.cat([F.one_hot(l_y, num_classes=num_classes).float(), u_y_pseudo], dim=0)
mixed_h, mixed_e, y_a, y_b, lam = mixup_data(all_h, all_e, all_y, alpha=config['mixup_alpha'], device=device)
# --- Forward Pass ---
logits, f_h, f_e = model(mixed_h, mixed_e)
# --- Loss Calculation ---
# Split the mixed batch back into labeled and unlabeled portions
labeled_batch_size = l_h.size(0)
# Supervised Loss (Cross-Entropy)
loss_ce = lam * ce_loss_fn(logits[:labeled_batch_size], y_a[:labeled_batch_size]) + \
(1 - lam) * ce_loss_fn(logits[:labeled_batch_size], y_b[:labeled_batch_size])
# Unsupervised Loss (L2)
pred_probs = torch.softmax(logits[labeled_batch_size:], dim=1)
loss_l2 = lam * l2_loss_fn(pred_probs, y_a[labeled_batch_size:]) + \
(1 - lam) * l2_loss_fn(pred_probs, y_b[labeled_batch_size:])
# Contrastive Loss (Triplet)
# Create negative pairs by shuffling E-features
shuffled_indices = torch.randperm(f_e.size(0)).to(device)
f_e_negative = f_e[shuffled_indices]
loss_ct = triplet_loss(f_h, f_e, f_e_negative, margin=config['contrastive_margin'])
# --- Total Loss ---
loss = loss_ce + config['lambda_u'] * loss_l2 + config['lambda_c'] * loss_ct
# --- Backward Pass and Optimization ---
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
total_ce_loss += loss_ce.item()
total_l2_loss += loss_l2.item()
total_ct_loss += loss_ct.item()
except StopIteration:
break
avg_loss = total_loss / num_batches
avg_ce = total_ce_loss / num_batches
avg_l2 = total_l2_loss / num_batches
avg_ct = total_ct_loss / num_batches
print(f"Epoch [{epoch+1}/{config['epochs']}], Avg Loss: {avg_loss:.4f}, "
f"CE Loss: {avg_ce:.4f}, L2 Loss: {avg_l2:.4f}, Contrastive Loss: {avg_ct:.4f}")
print("Training finished.")
if __name__ == '__main__':
# Hyperparameters from the paper and reasonable defaults
config = {
'epochs': 10,
'batch_size': 32, # Paper uses 64
'learning_rate': 1e-4,
'sharpen_temp': 0.5,
'mixup_alpha': 2.0,
'lambda_u': 7.5, # Weight for unlabeled L2 loss
'lambda_c': 0.1, # Weight for contrastive loss
'contrastive_margin': 37.0
}
train_model(config)
Related posts, You May like to read
- 7 Shocking Truths About Knowledge Distillation: The Good, The Bad, and The Breakthrough (SAKD)
- 7 Revolutionary Breakthroughs in Medical Image Translation (And 1 Fatal Flaw That Could Derail Your AI Model)
- 7 Revolutionary Breakthroughs in Small Object Detection: The DAHI Framework
- 1 Revolutionary Breakthrough in AI Object Detection: GridCLIP vs. Two-Stage Models