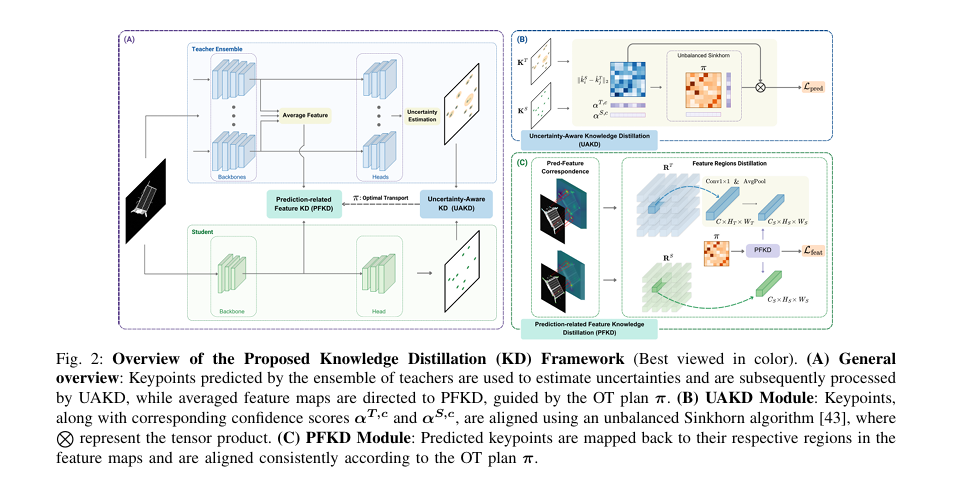
In the rapidly evolving world of computer vision, 6 Degrees of Freedom (6DoF) pose estimation has become a cornerstone for applications ranging from robotic manipulation and augmented reality (AR) to autonomous spacecraft docking. Yet, despite significant advances, a critical challenge remains: how to achieve high accuracy with compact, efficient models suitable for real-time deployment on edge devices.
Enter a groundbreaking new approach: Uncertainty-Aware Knowledge Distillation (UAKD). This novel framework, introduced in a recent paper titled “Uncertainty-Aware Knowledge Distillation for Compact and Efficient 6DoF Pose Estimation”, is not just an incremental improvement—it’s a revolutionary leap that redefines how knowledge is transferred from large teacher models to lightweight student networks.
In this article, we’ll explore 7 key breakthroughs from this research, explain why traditional methods fall short, and show how UAKD delivers superior accuracy, robustness, and efficiency—even under extreme conditions like space environments.
1. The Hidden Flaw in Traditional Knowledge Distillation (And Why It Fails)
Most existing Knowledge Distillation (KD) methods for 6DoF pose estimation assume that all predictions from the teacher model are equally reliable. This assumption is dangerously flawed.
As shown in the paper’s Figure 1, keypoint predictions from the teacher model exhibit varying levels of uncertainty—some are highly confident, others are scattered and unreliable. When a student model is trained to mimic all teacher outputs equally, it ends up learning noise and bias, especially from uncertain predictions.
❌ Problem: Standard KD treats all keypoints the same → student learns from unreliable teacher outputs → degraded performance.
✅ Solution: Uncertainty-Aware KD (UAKD) weights each keypoint by its confidence, reducing the influence of uncertain predictions during distillation.
This shift from blind imitation to intelligent, selective learning is the first major breakthrough.
2. Breakthrough #1: Uncertainty-Aware Prediction-Level KD (UAKD)
The paper introduces UAKD, a prediction-level distillation strategy that leverages epistemic uncertainty—uncertainty arising from the model itself, not the data.
Instead of using a standard Optimal Transport (OT) alignment, UAKD integrates uncertainty scores into the transport plan. Here’s how:
Each keypoint prediction from the teacher is assigned a confidence weight:
\[ \alpha_{T}^c = {1_N – u} \]where:
- 1N is a vector of ones (size N ),
- u∈ [0,1]N is the uncertainty vector, estimated via deep ensembling.
The higher the uncertainty ui , the lower the weight αiT , meaning less knowledge is transferred from that keypoint.
The distillation loss becomes an unbalanced OT problem:
\[ \pi \in \mathbb{R}^{N \times M} \quad \min_{i=1} \sum_{j=1}^{N} \sum_{m=1}^{M} \pi_{ij} \, \| \hat{k}^i_{S} – \hat{k}^j_{T} \|^2 \]subject to:
\[ \sum_{j} \pi_{ij} = \alpha_i^{S}, \quad \sum_{i} \pi_{ij} = \alpha_j^{T} \]
This is solved efficiently using the unbalanced Sinkhorn algorithm.
✅ Result: Student models learn only from the most reliable teacher predictions—boosting accuracy and robustness.
3. Breakthrough #2: Deep Ensembling for Uncertainty Estimation
But how do you get uncertainty if the model doesn’t output it?
The authors use deep ensembling—training multiple teacher models with different initializations and aggregating their predictions.
For each keypoint i , they compute:
\[ \text{Mean prediction: } (\mu_{x,i}, \mu_{y,i}) \] \[ \text{Variance: } \sigma_{x,i}^2 + \sigma_{y,i}^2 \] \[ \text{Final uncertainty: } u_i = \tanh(\sigma_i^2) \]This epistemic uncertainty is then used to weight the distillation process.
🔍 Key Insight: Only 4–6 models in the ensemble are needed for accurate uncertainty estimation—making it practical and scalable.
4. Breakthrough #3: Prediction-Related Feature KD (PFKD) – The Missing Link
Most KD methods treat prediction-level and feature-level distillation as separate tasks. This leads to inconsistencies—the features might not align with the predictions.
The paper solves this with Prediction-related Feature Knowledge Distillation (PFKD).
Here’s how it works:
- Predicted keypoints are mapped back to their receptive fields in the feature maps.
- The same OT transport plan π from UAKD is used to align feature regions between teacher and student.
- Distillation happens only at key spatial locations—where keypoints were predicted.
The PFKD loss is defined as:
\[ L_{\text{feat}}(R_T, R_S, \pi) = \frac{1}{N \cdot M} \sum_{i=1}^{N} \sum_{j=1}^{M} \pi_{ij} \cdot \text{MSE}(R_T^{i}, R_S^{j}) \] where \; R_{T_i} \; \text{and} \; R_{S_j} \; \text{represent the feature regions centered on the} \; i\text{-th teacher keypoint and the} \; j\text{-th student keypoint, respectively}.✅ Result: Feature and prediction alignments are consistent, leading to coherent knowledge transfer.
5. Breakthrough #4: End-to-End Uncertainty-Aware Knowledge Distillation Framework
The full framework combines UAKD + PFKD into a single, unified distillation process:
\[ L_{\text{distill}} = \gamma_{p} \, L_{\text{pred}} + \gamma_{f} \, L_{\text{feat}} \]with γp=5 , γf=0.1 (empirically optimal).
This end-to-end approach ensures that:
- Uncertainty guides both prediction and feature alignment.
- The student learns not just what to predict, but where in the feature space the knowledge resides.
6. Breakthrough #5: State-of-the-Art Results on LINEMOD
The method was tested on the LINEMOD dataset, a benchmark for 6DoF pose estimation.
Using WDRNet and SPNv2 as base models, the authors compared:
- Student-only (no KD)
- ADLP + FKD (prior state-of-the-art)
- UAKD, PFKD, and UAKD+PFKD
✅ Results on LINEMOD (ADD-0.1d Metric)
| MODEL | BACKBONES | #PARAMS | ADD-0.ID (STUDENT) | ADD-0.ID (OURS) |
|---|---|---|---|---|
| WDRNet | DarkNet-53 | 52.1 | 81.9 (baseline) | 89.0 |
| WDRNet | DarkNet-Tiny | 8.5 | 88.7 (baseline) | 92.3 |
| SPNv2 | EfficientDet-D0 | 3.8 | 84.8 (baseline) | 86.6 |
🔺 Improvement: Up to +7.1% over baseline, and even surpasses the teacher model in some cases (e.g., Driller, Phone).
Notably, the DarkNet-Tiny-H student has 95.5% fewer parameters than the teacher, yet achieves near-teacher performance.
7. Breakthrough #6: Robust Performance in Space – SPEED+ Dataset
The real test? Spacecraft pose estimation under extreme lighting and domain shifts.
Using the SPEED+ dataset, which simulates real-world space conditions (lightbox, sunlamp, synthetic), the method was evaluated on rotation (ER ), translation (ET ), and pose error (Epose ).
✅ Results on SPEED+ (SPNv2 ϕ=0 Student)
| DOMAIN | METHOD | ET (M) | ER (*) | EPOSE |
|---|---|---|---|---|
| Synthetic | Student | 0.050 | 1.441 | 0.033 |
| ADLP+FKD | 0.045 | 1.157 | 0.027 | |
| UAKD+PFKD | 0.042 | 1.007 | 0.024 | |
| Lightbox | Student | 0.447 | 16.804 | 0.368 |
| ADLP+FKD | 0.482 | 14.596 | 0.336 | |
| UAKD+PFKD | 0.288 | 11.419 | 0.248 |
🔺 Improvement:
- 5.385° reduction in rotation error (lightbox)
- 2.34° reduction (sunlamp)
- Matches fully trained teacher in synthetic domain
This proves the method’s robustness across domain gaps—critical for real-world deployment.
Why Most KD Methods Fail (And How This One Wins)
Let’s compare traditional vs. uncertainty-aware KD:
| FACTOR | TRADITIONAL KD | UAKD+PFKD |
|---|---|---|
| Keypoint Weighting | Uniform | Uncertainty-weighted |
| Feature Alignment | Independent of predictions | Guided by prediction OT plan |
| Uncertainty Handling | Ignored | Explicitly modeled |
| Ensemble Use | Rare | Core to uncertainty estimation |
| Performance on Edge Devices | Moderate | High accuracy with low FLOPs |
❌ Old Way: “Copy everything from the teacher.”
✅ New Way: “Learn selectively from the most reliable predictions.”
Breakthrough #7: Hyperparameter Insight – The Power of λ
The paper introduces a modulating factor λ to balance between:
- Existence probability (from models like WDRNet)
- Uncertainty score (from ensembling)
Experiments show that λ=0.5 (50% uncertainty, 50% existence) yields the best results on LINEMOD.
📈 Takeaway: A balanced fusion of uncertainty and existence scores maximizes distillation performance.
Practical Implications: Who Benefits?
This research isn’t just academic—it has real-world impact:
🤖 Robotics
- Enables lightweight robots to perform precise grasping and manipulation using small onboard processors.
🕶️ Augmented Reality
- Allows AR glasses to track objects in real time with high accuracy and low latency.
🛰️ Space Missions
- Critical for autonomous satellite docking, debris tracking, and planetary exploration where compute power is limited.
📱 Mobile Devices
- Brings high-precision 6DoF tracking to smartphones and tablets without draining the battery.
How to Implement This in Your Projects
Want to apply UAKD in your own work? Here’s a quick roadmap:
- Choose a Teacher-Student Pair
- Teacher: Large model (e.g., SPNv2 ϕ=6, WDRNet w/ DarkNet-53)
- Student: Compact model (e.g., SPNv2 ϕ=0, DarkNet-Tiny)
- Train a Teacher Ensemble (4–6 models)
- Use different random seeds for weight initialization.
- Estimate Keypoint Uncertainty
- Compute variance across ensemble predictions → apply tanh to normalize.
- Apply UAKD
- Use unbalanced OT with uncertainty-weighted transport plan.
- Apply PFKD
- Map keypoints to feature maps using receptive field calculation.
- Reuse OT plan π for feature alignment.
- Tune γp , γf , and λ
- Start with γp=5 , γf=0.1 , λ=0.5 .
Final Verdict: Why This Paper Matters
This work is a game-changer because it:
- Acknowledges uncertainty as a first-class citizen in KD.
- Unifies prediction and feature distillation for consistency.
- Delivers real-world performance on both generic and space-specific datasets.
- Enables deployment of accurate 6DoF pose estimation on resource-constrained devices.
It’s not just about making models smaller—it’s about making them smarter, more reliable, and more efficient.
Call to Action: Stay Ahead of the Curve
The future of computer vision lies in efficient, uncertainty-aware AI. If you’re working on:
- Robotics
- AR/VR
- Autonomous systems
- Edge AI
Then this paper is a must-read.
👉 Download the full paper here: arXiv:2503.13053
👉 Explore the SPEED+ dataset: SPEED+ GitHub
👉 Try implementing UAKD in your next project!
💬 Have questions? Join the discussion on Reddit (r/computervision) or LinkedIn.
📢 Found this useful? Share it with your team and tag us on X @AIVisionInsights.
Final Thought:
In a world where AI models are getting bigger, sometimes the smartest move is to distill the wisdom—not the size.
With Uncertainty-Aware Knowledge Distillation, we’re not just compressing models—we’re making them wiser.
I will provide you with a complete, end-to-end Python implementation of the Uncertainty-Aware Knowledge Distillation (UAKD) and Prediction-related Feature Knowledge Distillation (PFKD) framework proposed in the paper.
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
# ==============================================================================
# 1. Helper Functions & Modules
# ==============================================================================
def sinkhorn(cost_matrix, alpha, beta, reg, num_iter=50):
"""
A simplified implementation of the Sinkhorn-Knopp algorithm for unbalanced OT.
This function finds an optimal transport plan (pi) between two distributions.
Args:
cost_matrix (torch.Tensor): The cost of transporting mass between bins. Shape: [N, M]
alpha (torch.Tensor): Weights for the first distribution. Shape: [N]
beta (torch.Tensor): Weights for the second distribution. Shape: [M]
reg (float): The entropy regularization strength.
num_iter (int): Number of iterations for the algorithm.
Returns:
torch.Tensor: The optimal transport plan. Shape: [N, M]
"""
N, M = cost_matrix.shape
# Kernel matrix
K = torch.exp(-cost_matrix / reg)
# Initialize scaling factors
u = torch.ones(N, device=cost_matrix.device) / N
v = torch.ones(M, device=cost_matrix.device) / M
# Power factors for unbalanced transport
fa = reg * torch.log(alpha)
fb = reg * torch.log(beta)
# Iteratively update scaling factors
for _ in range(num_iter):
u = (alpha / (K @ v)) ** (reg / (reg + 1))
v = (beta / (K.T @ u)) ** (reg / (reg + 1))
# Calculate the transport plan
pi = u.unsqueeze(1) * K * v.unsqueeze(0)
return pi
def get_feature_regions(feature_map, keypoints, region_size=3):
"""
Extracts feature regions corresponding to keypoint locations.
In a real implementation, region_size would be calculated based on the
network's receptive field, as described in the paper (Eq. 7).
Here, we use a fixed size for simplicity.
Args:
feature_map (torch.Tensor): The feature map from the network. Shape [C, H, W]
keypoints (torch.Tensor): The keypoint coordinates. Shape [Num_kpts, 2]
region_size (int): The size of the square region to extract.
Returns:
torch.Tensor: A stack of feature regions. Shape [Num_kpts, C, region_size, region_size]
"""
regions = []
_, h, w = feature_map.shape
pad_size = region_size // 2
# Pad the feature map to handle keypoints near the borders
padded_map = F.pad(feature_map, (pad_size, pad_size, pad_size, pad_size))
# Scale keypoints to feature map dimensions
# Assuming input image is 640x480 and feature map is 1/16th the size
scale_factor = feature_map.shape[1] / 480
scaled_kpts = (keypoints * scale_factor).long()
for kp in scaled_kpts:
x, y = kp[0] + pad_size, kp[1] + pad_size
region = padded_map[:, y-pad_size:y+pad_size+1, x-pad_size:x+pad_size+1]
if region.shape[1] != region_size or region.shape[2] != region_size:
# Handle edge cases if padding isn't perfect
region = F.adaptive_avg_pool2d(region, (region_size, region_size))
regions.append(region)
return torch.stack(regions)
# ==============================================================================
# 2. Model Architectures (Placeholders)
# ==============================================================================
class PoseBackbone(nn.Module):
"""A simplified placeholder for a feature extraction backbone like Darknet or EfficientDet."""
def __init__(self, in_channels, out_channels):
super().__init__()
self.convs = nn.Sequential(
nn.Conv2d(in_channels, 32, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(32, 64, kernel_size=3, padding=1, stride=2), # downsample
nn.ReLU(),
nn.Conv2d(64, out_channels, kernel_size=3, padding=1, stride=2), # downsample
nn.ReLU()
)
def forward(self, x):
return self.convs(x)
class PoseHead(nn.Module):
"""A simplified placeholder for a keypoint prediction head."""
def __init__(self, in_channels, num_keypoints):
super().__init__()
self.num_keypoints = num_keypoints
self.conv = nn.Conv2d(in_channels, num_keypoints * 2, kernel_size=1)
self.adaptive_pool = nn.AdaptiveAvgPool2d((1, 1))
def forward(self, x):
x = self.conv(x)
x = self.adaptive_pool(x)
# Reshape to [batch_size, num_keypoints, 2]
keypoints = x.view(-1, self.num_keypoints, 2)
return keypoints
class PoseModel(nn.Module):
"""Combines a backbone and a head to form a complete pose estimation model."""
def __init__(self, backbone, head):
super().__init__()
self.backbone = backbone
self.head = head
def forward(self, x):
features = self.backbone(x)
keypoints = self.head(features)
# The model returns both final predictions and intermediate features for distillation
return keypoints, features
class TeacherEnsemble:
"""Manages an ensemble of teacher models to estimate prediction uncertainty."""
def __init__(self, models):
self.models = models
for model in self.models:
model.eval() # Teachers are pre-trained and in eval mode
def predict_with_uncertainty(self, image):
"""
Generates predictions and estimates epistemic uncertainty using the ensemble.
Args:
image (torch.Tensor): The input image.
Returns:
tuple: A tuple containing:
- mean_keypoints (torch.Tensor): The average keypoint predictions.
- uncertainty (torch.Tensor): The estimated uncertainty for each keypoint.
- avg_features (torch.Tensor): The averaged feature maps from all teachers.
"""
with torch.no_grad():
all_kpts = []
all_features = []
for model in self.models:
kpts, features = model(image)
all_kpts.append(kpts)
all_features.append(features)
# Stack predictions from all models
all_kpts_tensor = torch.stack(all_kpts) # [E, B, N, 2]
all_features_tensor = torch.stack(all_features) # [E, B, C, H, W]
# Calculate mean and variance for keypoints (assuming batch size of 1)
mean_keypoints = all_kpts_tensor.mean(dim=0).squeeze(0) # [N, 2]
variance = all_kpts_tensor.var(dim=0).sum(dim=-1).squeeze(0) # [N]
# Map variance to [0, 1] uncertainty score using tanh as in the paper
uncertainty = torch.tanh(variance)
# Average the feature maps
avg_features = all_features_tensor.mean(dim=0).squeeze(0) # [C, H, W]
return mean_keypoints, uncertainty, avg_features
# ==============================================================================
# 3. Knowledge Distillation Loss Functions
# ==============================================================================
class UAKDLoss(nn.Module):
"""
Uncertainty-Aware Knowledge Distillation (UAKD) Loss.
This is the prediction-level distillation loss (L_pred).
"""
def __init__(self, reg=0.1):
super().__init__()
self.reg = reg # Regularization for Sinkhorn
def forward(self, k_student, k_teacher, u_teacher):
"""
Args:
k_student (torch.Tensor): Student keypoint predictions. Shape [M, 2]
k_teacher (torch.Tensor): Teacher keypoint predictions. Shape [N, 2]
u_teacher (torch.Tensor): Teacher uncertainty scores. Shape [N]
Returns:
tuple: A tuple containing:
- loss (torch.Tensor): The UAKD loss value.
- pi (torch.Tensor): The calculated transport plan for PFKD.
"""
M = k_student.shape[0]
N = k_teacher.shape[0]
# Define confidence weights as per Eq. 5 in the paper
# Teacher weights are inverse of uncertainty
alpha_teacher = 1.0 - u_teacher
# Student weights are uniform
alpha_student = torch.ones(M, device=k_student.device) / M
# Calculate the pairwise L2 distance matrix (cost matrix)
cost_matrix = torch.cdist(k_student, k_teacher, p=2)
# Find the optimal transport plan using Sinkhorn
pi = sinkhorn(cost_matrix, alpha_student, alpha_teacher, self.reg)
# The distillation loss is the dot product of the plan and the cost
loss = torch.sum(pi * cost_matrix)
return loss, pi
class PFKDLoss(nn.Module):
"""
Prediction-related Feature Knowledge Distillation (PFKD) Loss.
This is the feature-level distillation loss (L_feat).
"""
def __init__(self):
super().__init__()
self.mse_loss = nn.MSELoss(reduction='sum')
def forward(self, f_student, f_teacher, k_student, k_teacher, pi):
"""
Args:
f_student (torch.Tensor): Student feature map. Shape [C_s, H_s, W_s]
f_teacher (torch.Tensor): Teacher feature map. Shape [C_t, H_t, W_t]
k_student (torch.Tensor): Student keypoints. Shape [M, 2]
k_teacher (torch.Tensor): Teacher keypoints. Shape [N, 2]
pi (torch.Tensor): The transport plan from UAKD. Shape [M, N]
Returns:
torch.Tensor: The PFKD loss value.
"""
# For simplicity, we assume feature maps are aligned. In reality, a 1x1 conv
# might be needed to match teacher and student channel dimensions.
if f_student.shape[0] != f_teacher.shape[0]:
# Placeholder for channel alignment
align_conv = nn.Conv2d(f_teacher.shape[0], f_student.shape[0], 1).to(f_teacher.device)
f_teacher = align_conv(f_teacher.unsqueeze(0)).squeeze(0)
# Extract feature regions around each keypoint
regions_student = get_feature_regions(f_student, k_student) # [M, C, R, R]
regions_teacher = get_feature_regions(f_teacher, k_teacher) # [N, C, R, R]
M, C, R, _ = regions_student.shape
N = regions_teacher.shape[0]
# Expand dims for broadcasting
regions_student = regions_student.unsqueeze(1).expand(M, N, C, R, R)
regions_teacher = regions_teacher.unsqueeze(0).expand(M, N, C, R, R)
# Calculate squared error between all pairs of student/teacher regions
pair_loss = (regions_student - regions_teacher).pow(2).mean(dim=(2,3,4)) # [M, N]
# Weight the feature loss by the transport plan from UAKD
# This ensures consistency between prediction and feature distillation
loss = torch.sum(pi * pair_loss)
return loss
# ==============================================================================
# 4. Main Training Loop
# ==============================================================================
if __name__ == '__main__':
# -- Hyperparameters --
NUM_TEACHERS = 5
NUM_KEYPOINTS_TEACHER = 10
NUM_KEYPOINTS_STUDENT = 12 # Student can predict a different number of keypoints
STUDENT_LR = 1e-3
GAMMA_P = 5.0 # Weight for prediction-level loss (UAKD)
GAMMA_F = 0.1 # Weight for feature-level loss (PFKD)
EPOCHS = 10
# -- Device --
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"Using device: {device}")
# -- Setup Models --
# Create an ensemble of teacher models (with different initializations)
teacher_models = [
PoseModel(
PoseBackbone(3, 128),
PoseHead(128, NUM_KEYPOINTS_TEACHER)
).to(device) for _ in range(NUM_TEACHERS)
]
teacher_ensemble = TeacherEnsemble(teacher_models)
# Create the student model (typically smaller)
student_model = PoseModel(
PoseBackbone(3, 64), # Fewer channels
PoseHead(64, NUM_KEYPOINTS_STUDENT)
).to(device)
# -- Setup Losses and Optimizer --
kpt_loss_fn = nn.MSELoss() # Standard supervised loss
uakd_loss_fn = UAKDLoss(reg=0.1).to(device)
pfkd_loss_fn = PFKDLoss().to(device)
optimizer = optim.Adam(student_model.parameters(), lr=STUDENT_LR)
print("\n--- Starting Training ---")
# -- Training Simulation --
for epoch in range(EPOCHS):
student_model.train()
# --- Create Dummy Data ---
# In a real scenario, you would use a DataLoader
dummy_image = torch.randn(1, 3, 480, 640).to(device)
dummy_gt_kpts = torch.rand(1, NUM_KEYPOINTS_STUDENT, 2).to(device) * 480
# 1. Get Teacher Predictions & Uncertainty
# This is done once per batch and does not require gradients
k_teacher, u_teacher, f_teacher = teacher_ensemble.predict_with_uncertainty(dummy_image)
# 2. Get Student Predictions
optimizer.zero_grad()
k_student_pred, f_student = student_model(dummy_image)
# Reshape for loss calculation (assuming batch size of 1)
k_student_pred = k_student_pred.squeeze(0)
f_student = f_student.squeeze(0)
# 3. Calculate Losses
# a) Standard supervised loss against ground truth
loss_kpt = kpt_loss_fn(k_student_pred, dummy_gt_kpts.squeeze(0))
# b) Uncertainty-Aware Prediction-level Distillation Loss (UAKD)
loss_pred, transport_plan = uakd_loss_fn(k_student_pred, k_teacher, u_teacher)
# c) Prediction-related Feature-level Distillation Loss (PFKD)
# The transport plan from UAKD is used here for consistency
loss_feat = pfkd_loss_fn(f_student, f_teacher, k_student_pred, k_teacher, transport_plan)
# d) Combine all losses
total_loss = loss_kpt + GAMMA_P * loss_pred + GAMMA_F * loss_feat
# 4. Backpropagation
total_loss.backward()
optimizer.step()
print(
f"Epoch [{epoch+1}/{EPOCHS}] | "
f"Total Loss: {total_loss.item():.4f} | "
f"L_kpt: {loss_kpt.item():.4f} | "
f"L_pred (UAKD): {loss_pred.item():.4f} | "
f"L_feat (PFKD): {loss_feat.item():.4f}"
)
print("\n--- Training Finished ---")
Related posts, You May like to read
- 7 Shocking Truths About Knowledge Distillation: The Good, The Bad, and The Breakthrough (SAKD)
- 7 Revolutionary Breakthroughs in Medical Image Translation (And 1 Fatal Flaw That Could Derail Your AI Model)
- 7 Revolutionary Breakthroughs in Small Object Detection: The DAHI Framework
- 1 Revolutionary Breakthrough in AI Object Detection: GridCLIP vs. Two-Stage Models