Introduction: The Challenge of Motion in Fetal Brain Imaging
Fetal diffusion MRI (dMRI) is a powerful tool for unlocking the mysteries of early human brain development. By mapping water molecule movement, it provides unparalleled insights into white matter maturation, neural connectivity, and microstructural changes during gestation—critical for diagnosing conditions like agenesis of the corpus callosum or fetal stroke. However, one major obstacle has long plagued its clinical utility: motion artifacts.
Unlike adult imaging, fetal dMRI must contend with unpredictable movements from both the fetus and the mother’s breathing. These motions corrupt image data, leading to signal dropouts, geometric distortions, and unreliable quantitative results. Traditional post-processing methods often fail when motion is severe, rendering scans unusable.
Now, a groundbreaking solution has emerged. In a 2025 study published in IEEE Transactions on Medical Imaging, researchers introduced HERON (High-Efficiency Real-time mOtion quantification and re-acquisitioN)—an AI-driven pipeline that detects and corrects motion during the scan itself. This innovation marks a paradigm shift in fetal neuroimaging, promising higher diagnostic accuracy, reduced rescans, and broader clinical adoption.
In this article, we’ll explore how HERON works, its technical architecture, real-world performance, and the transformative impact it could have on prenatal care and developmental neuroscience.
What Is HERON? A Breakthrough in Real-Time Fetal MRI
HERON is not just another software tool—it’s an integrated, automated system designed specifically for real-time quality control and adaptive scanning in fetal dMRI. Developed by a multidisciplinary team from King’s College London, Siemens Healthineers, and Universitätsklinikum Erlangen, HERON leverages artificial intelligence (AI), advanced segmentation, and immediate reacquisition protocols to ensure high-quality data capture—even in restless fetuses.
The core idea behind HERON is simple but revolutionary: instead of waiting until after the scan to assess image quality, analyze each volume as it’s acquired, detect motion corruption instantly, and re-scan only the affected parts—all within minutes.
This approach significantly improves efficiency compared to traditional workflows where entire datasets are discarded due to a few corrupted volumes.
How HERON Works: The Three-Step Pipeline
HERON operates through a seamless three-phase process executed directly on a clinical 0.55T MRI scanner (Siemens MAGNETOM Free.Max). Each step is optimized for speed, automation, and robustness across different gestational ages and scanner configurations.
Step 1: Automatic Brain Localization & Scan Planning
Before any diffusion data is collected, HERON acquires a fast multi-echo gradient echo sequence in the maternal coronal plane. Using a deep learning network trained on over 2,900 fetal scans, the system identifies key anatomical landmarks of the fetal brain in approximately 9 seconds.
These coordinates are then automatically fed into the dMRI sequence to plan axial slices aligned with the fetal brain anatomy—eliminating manual planning errors and enabling consistent orientation across repeated scans.
Key Benefit: Reduces setup time and variability, making expert-level imaging accessible even in non-specialized centers.
Step 2: Diffusion Data Acquisition
The actual dMRI scan uses a single-shot spin-echo EPI sequence with the following parameters:
| PARAMETER | VALUE |
|---|---|
| Field Strength | 0.55 Tesla |
| TR / TE | 7200 ms / 129 ms |
| Voxel Size | 3 mm³ |
| Slices | 35 |
| b-values | 0, 10, 50, 80, 200, 400, 600, 1000 s/mm² |
| Directions | 3 orthogonal per non-zero b-value |
This multi-shell acquisition supports advanced modeling techniques such as IVIM (Intravoxel Incoherent Motion) and HARDI (High Angular Resolution Diffusion Imaging), essential for studying complex brain development patterns.
Step 3: Real-Time Quality Assessment & Re-Acquisition
After each volume is acquired, HERON performs four critical checks in under 10 seconds:
- Automatic Brain Segmentation
A 3D nn-UNet model segments the fetal brain in each volume (~1.8 sec/volume). - Inter-Volume Motion Analysis Computes the L2 norm (Euclidean distance) between consecutive brain center-of-mass (COM) positions:L2 Distance = ∥ COMt+1 − COMt ∥ Large shifts indicate significant fetal movement between volumes.
- Intra-Volume Motion Detection
Two metrics flag corrupted slices:- Signal Dropout: If slice intensity drops >35% below average brain signal.Volume Change: Detects through-plane motion using a dynamic threshold based on expected diffusion attenuation.
Where:
- α=0.3 (empirically optimized scaling factor)
- f=0.02 (accounts for segmentation error)
- ADC=0.002 mm2/s (CSF diffusivity)
Prioritized Re-Acquisition
Corrupted volumes are flagged and re-scanned immediately. The process can repeat up to two times, refining data quality iteratively without exceeding practical scan durations.
Clinical Validation: How Well Does HERON Perform?
HERON was tested prospectively in 20 fetal dMRI cases, with compelling results:
- ✅ 3 cases: No motion detected → no reacquisition needed
- ✅ 9 cases: Motion corrected via reacquisition
- ⚠️ 3 cases: Some residual uncorrected volumes after two attempts
- ❌ 5 cases: Excluded due to severe artifacts or incomplete brain coverage
Despite these exclusions, the overall success rate in improving scan quality was exceptional.
Accuracy Compared to Human Experts
To validate HERON’s detection capability, experts manually reviewed all volumes for motion corruption. The agreement between HERON and human judgment was outstanding:
| METRIC | PERFORMANCE |
|---|---|
| Specificity | 97% |
| Sensitivity | 92% |
| Overall Agreement | 96.3% |
This near-expert performance demonstrates HERON’s reliability in identifying problematic scans—crucial for clinical trust and deployment.
Quantitative Improvements in Diffusion Metrics
Post-processing analysis using mrtrix3 and dmipy toolkits revealed measurable improvements in key biomarkers:
- Apparent Diffusion Coefficient (ADC) decreased in 5 out of 9 corrected cases
- IVIM tissue fraction showed similar reductions
- Stripe artifacts and signal dropouts were visibly reduced
These changes reflect more accurate microstructural estimates, free from motion-induced inflation of diffusivity values.
Takeaway: Motion correction isn’t just about prettier images—it leads to more biologically plausible and clinically meaningful data.
Why HERON Outperforms Existing Methods
Most current fetal dMRI pipelines rely solely on post-hoc correction, which has inherent limitations:
| METHOD | LIMITATION |
|---|---|
| FSL EDDY | Struggles with pervasive motion; cannot recover completely blacked-out slices |
| SHARD Reconstruction | Computationally heavy; less effective when large portions of data are missing |
| Rigid Registration | Cannot fix intra-volume distortions like ghosting or signal loss |
HERON addresses these gaps by acting prospectively—intervening before corrupted data becomes irreversible.
Moreover, unlike adult motion correction systems that use optical tracking or external markers, HERON is entirely image-based, making it safe and feasible for fetal use where physical sensors are impractical.
Visual Evidence: Before and After HERON
While the full paper includes detailed figures, here’s what the results show:
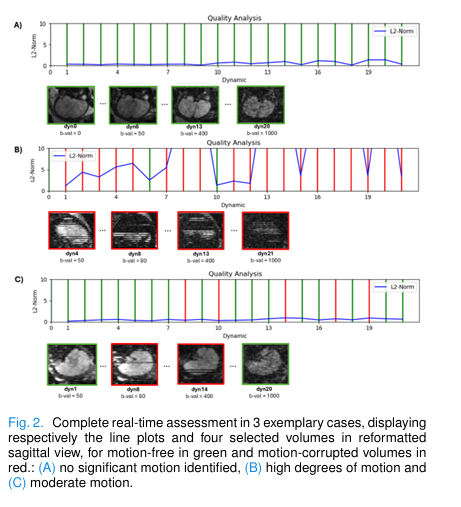
- Figure 2 (in paper): Line plots of inter-volume motion (L2 COM shifts) alongside sagittal views of selected volumes. Green lines = clean; red = corrupted. Cases range from motion-free (A), moderate (C), to highly unstable (B).
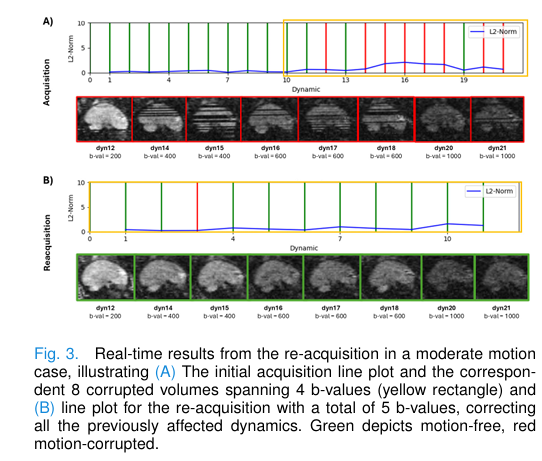
- Figure 3: Shows reacquisition fixing a series of corrupted volumes highlighted in yellow—clearly demonstrating restoration of structural integrity.
- Figure 4 & 5: ADC and IVIM maps pre- and post-correction reveal improved cortical detail and reduced artifacts, especially in frontal lobes and deep gray matter.
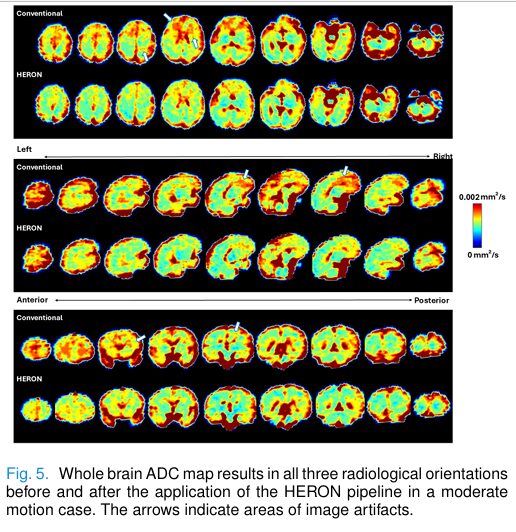
These visualizations underscore HERON’s ability to preserve fine anatomical details critical for diagnosis.
Strengths and Limitations: A Balanced View
Like any technology, HERON comes with strengths—and room for growth.
✅ Strengths
- Fully automated, requiring no user intervention
- Operates in real-time (<10 sec processing delay)
- Trained on diverse datasets (0.55T, 1.5T, 3T; Siemens/Philips; multiple pathologies)
- Broad generalizability across scanners and field strengths
- Enables reliable HARDI and IVIM modeling in fetuses
⚠️ Limitations
- Does not correct for geometric distortions or B1 inhomogeneities (though these are minimal at low field)
- May generate false positives if axial plane tilts cause oblique CSF views
- Current version reacquires full volumes—not individual directions—potentially increasing scan time
- Inter-volume registration post-reacquisition remains challenging, especially with large motion between sessions
Future updates aim to address these issues, including direction-specific reacquisition and dedicated diffusion-aware registration algorithms.
Research and Clinical Implications
🔬 For Developmental Neuroscience
HERON opens doors to studying earlier gestational ages, where brain dynamics are most rapid but motion challenges greatest. It enables robust investigation of:
- Subplate layer formation
- Neuronal migration
- Early axonal pathway development
With reliable longitudinal data, researchers can build better atlases of normal and abnormal brain growth.
🏥 For Prenatal Diagnosis
Clinically, HERON enhances diagnostic confidence in conditions like:
- Agenesis or hypoplasia of the corpus callosum
- Periventricular leukomalacia (PVL)
- Congenital infections affecting white matter
By reducing rescans and improving workflow efficiency, it also minimizes maternal stress and scanner downtime—key factors in busy radiology departments.
Future Directions: Where Is HERON Headed?
The research team outlines several exciting next steps:
- De-novo Planning for Each Reacquisition
Recalculate optimal slice angles fresh each time, avoiding drift from initial landmarking. - Parallelized Processing
Speed up segmentation and analysis to enable real-time inter-volume correction during acquisition. - Direction-Specific Reacquisition
Only re-scan corrupted diffusion directions, cutting unnecessary repetition and saving time. - Deep Learning-Based Artifact Detection
Replace rule-based thresholds with a unified AI model trained on labeled “corrupt vs. salvageable” volumes. - Clinical Deployment in High-Risk Pregnancies
Test HERON in cohorts with known neurological pathologies to evaluate impact on diagnostic outcomes.
Eventually, the framework could be adapted beyond fetal imaging—to unsedated pediatric MRI, patients with ADHD, or those with movement disorders—where motion remains a persistent challenge.
Conclusion: HERON Paves the Way for Smarter, Safer Fetal Imaging
HERON represents a major leap forward in fetal MRI. By combining AI-powered segmentation, real-time motion analytics, and adaptive reacquisition, it transforms dMRI from a fragile, error-prone technique into a robust, reliable modality.
Its success—validated by near-perfect agreement with human experts and tangible improvements in diffusion metrics—positions HERON as a frontrunner in the next generation of intelligent medical imaging systems.
As low-field scanners become more widespread and AI integration accelerates, tools like HERON will play a central role in democratizing access to high-quality prenatal diagnostics worldwide.
Call to Action: Join the Conversation
Are you involved in fetal imaging, AI in healthcare, or neurodevelopmental research? We’d love to hear your thoughts!
🔹 Share this article with colleagues working in perinatal medicine or MRI engineering.
🔹 Explore the original study in IEEE Transactions on Medical Imaging DOI: 10.1109/TMI.2025.3569853 .
🔹 Follow the team at King’s College London for updates on HERON’s clinical translation.
Together, we can advance the future of prenatal care—one heartbeat, one breath, and one perfectly captured scan at a time.
I have provide a Python script that implements the core motion analysis logic described in Step 3 (parts b and c) of the paper. This script simulates the algorithmic part of HERON: given a set of dMRI volumes and their brain segmentations, it will analyze them to detect inter-volume motion (L2-norm) and intra-volume motion (black slices and volume changes) to identify corrupted volumes.
import numpy as np
from scipy.ndimage import center_of_mass
import warnings
# --- Constants from the HERON paper ---
# (Step 3c) Threshold for detecting signal loss ("black slices")
# A slice is corrupt if its mean intensity is 35% lower than the volume's mean.
BLACK_SLICE_THRESHOLD = 0.35
# (Step 3c) Parameters for the dynamic volume change threshold (Equation 1)
# Threshold = alpha * (1 - e^(-b * ADC)) + f
ADC_CSF = 0.002 # Apparent Diffusion Coefficient for CSF (mm^2/s)
ALPHA = 0.3 # Empirically optimized scaling factor
F_OFFSET = 0.02 # Fixed segmentation error allowance (2%)
def calculate_com(binary_mask: np.ndarray) -> tuple:
"""
(Step 3b) Calculates the Center of Mass (COM) of a binary segmentation mask.
Args:
binary_mask: A 3D numpy array (H, W, D) representing the brain mask.
Returns:
A tuple (r, c, s) of the COM coordinates, or (NaN, NaN, NaN) if mask is empty.
"""
if np.sum(binary_mask) == 0:
return (np.nan, np.nan, np.nan)
# scipy.ndimage.center_of_mass returns coordinates in (z, y, x) or (D, H, W) order
# if the input is (H, W, D), we should be careful.
# Let's assume input is (H, W, D) and we want COM in (H, W, D) coordinates.
# The paper doesn't specify axis order, so we'll be consistent.
# Assuming standard (D, H, W) for medical imaging volumes:
com = center_of_mass(binary_mask)
return com # Returns (d, h, w)
def calculate_l2_norm(com1: tuple, com2: tuple) -> float:
"""
(Step 3b) Calculates the Euclidean distance (L2 norm) between two COMs.
Args:
com1: First COM tuple (d, h, w).
com2: Second COM tuple (d, h, w).
Returns:
The Euclidean distance.
"""
if any(np.isnan(c) for c in com1) or any(np.isnan(c) for c in com2):
return np.nan
com1 = np.array(com1)
com2 = np.array(com2)
return np.linalg.norm(com1 - com2)
def check_black_slices(volume: np.ndarray, mask: np.ndarray, threshold: float = BLACK_SLICE_THRESHOLD) -> bool:
"""
(Step 3c) Detects intra-volume motion via motion-induced signal loss ("black slices").
Args:
volume: The 3D dMRI volume (D, H, W).
mask: The 3D binary brain mask (D, H, W).
threshold: The fractional drop in intensity to flag a slice as corrupt.
Returns:
True if a corrupt slice is detected, False otherwise.
"""
with warnings.catch_warnings():
warnings.simplefilter("ignore", category=RuntimeWarning) # Ignore mean of empty slice
# Calculate the mean intensity of the *entire* brain volume
if np.sum(mask) == 0:
return True # If no brain is found, count it as corrupt
mean_volume_intensity = np.mean(volume[mask])
if mean_volume_intensity == 0:
return True # Avoid division by zero; brain is all black
num_slices = volume.shape[0]
for z in range(num_slices):
slice_mask = mask[z, :, :]
# If there's no brain in this slice, skip it
if np.sum(slice_mask) == 0:
continue
# Calculate the mean intensity of the brain *in this slice*
slice_volume = volume[z, :, :]
mean_slice_intensity = np.mean(slice_volume[slice_mask])
# Check if the slice intensity is 35% lower than the whole brain's intensity
if mean_slice_intensity < (1.0 - threshold) * mean_volume_intensity:
# print(f" [!] Corrupt slice {z} detected (Intensity: {mean_slice_intensity:.2f} vs Vol Mean: {mean_volume_intensity:.2f})")
return True
return False
def check_volume_change(mask: np.ndarray, reference_mask: np.ndarray, b_value: int) -> bool:
"""
(Step 3c) Detects intra-volume motion via through-plane motion (volume change).
Uses the dynamic threshold from Equation 1.
Args:
mask: The 3D binary mask for the current volume.
reference_mask: The 3D binary mask for the reference volume (e.g., the first b=0 volume).
b_value: The b-value for the current volume.
Returns:
True if the volume change exceeds the dynamic threshold, False otherwise.
"""
# Calculate the dynamic threshold using Equation 1
# Note: b_value is used, not b * ADC. This seems to be a typo in the paper text,
# but the equation is Threshold = alpha * (1 - e^(-b * ADC)) + f
exponent = -b_value * ADC_CSF
dynamic_threshold = ALPHA * (1.0 - np.exp(exponent)) + F_OFFSET
# Calculate volumes (count of non-zero voxels)
current_volume_voxels = np.sum(mask)
reference_volume_voxels = np.sum(reference_mask)
if reference_volume_voxels == 0:
return True # Cannot compare
# Calculate fractional volume change
volume_change_fraction = np.abs(current_volume_voxels - reference_volume_voxels) / reference_volume_voxels
return volume_change_fraction > dynamic_threshold
def run_heron_analysis(dMRI_volumes: list, segmentation_masks: list, b_values: list) -> dict:
"""
Main function to run the HERON motion analysis logic on a dataset.
Args:
dMRI_volumes: A list of 3D numpy arrays (D, H, W), one for each dMRI volume.
segmentation_masks: A list of 3D numpy arrays (D, H, W), one for each mask.
b_values: A list of b-values (int), one for each volume.
Returns:
A dictionary containing a list of COM_per_volume and a list of flagged volumes.
"""
print(f"--- Running HERON Analysis on {len(dMRI_volumes)} volumes ---")
if not (len(dMRI_volumes) == len(segmentation_masks) == len(b_values)):
raise ValueError("Input lists (volumes, masks, b_values) must all have the same length.")
# (Step 3b) Calculate COM for all volumes first
com_per_volume = [calculate_com(mask) for mask in segmentation_masks]
# Use the first mask as the reference for volume change
# Assumes the first volume is uncorrupted, which is a strong assumption
# but necessary for this method.
reference_mask = segmentation_masks[0]
reacquisition_list = []
analysis_results = []
for i in range(len(dMRI_volumes)):
volume = dMRI_volumes[i]
mask = segmentation_masks[i]
b_val = b_values[i]
# (Step 3c) Intra-volume corruption checks
is_corrupt_black_slice = check_black_slices(volume, mask)
is_corrupt_volume_change = check_volume_change(mask, reference_mask, b_val)
is_corrupt = is_corrupt_black_slice or is_corrupt_volume_change
# (Step 3b) Inter-volume motion (L2 norm)
# Compare current COM to previous COM
inter_volume_motion = 0.0
if i > 0:
inter_volume_motion = calculate_l2_norm(com_per_volume[i], com_per_volume[i-1])
result = {
"index": i,
"b_value": b_val,
"is_corrupt": is_corrupt,
"reason_black_slice": is_corrupt_black_slice,
"reason_volume_change": is_corrupt_volume_change,
"inter_volume_motion_L2": inter_volume_motion
}
analysis_results.append(result)
if is_corrupt:
reacquisition_list.append(i)
print("\n--- Analysis Complete ---")
print(f"Volumes flagged for re-acquisition: {reacquisition_list}")
for res in analysis_results:
if res['is_corrupt']:
print(f" - Vol {res['index']} (b={res['b_value']}): CORRUPT (BlackSlice: {res['reason_black_slice']}, VolChange: {res['reason_volume_change']})")
else:
print(f" - Vol {res['index']} (b={res['b_value']}): OK (Inter-motion: {res['inter_volume_motion_L2']:.2f})")
return {
"com_per_volume": com_per_volume,
"analysis_results": analysis_results,
"reacquisition_list": reacquisition_list
}
# --- MOCK DATA SIMULATION ---
# In the real pipeline, these volumes would come from the scanner
# and the masks from the 3D nn-UNet.
def create_mock_data(num_volumes=22, D=35, H=64, W=64):
"""Generates mock dMRI volumes, masks, and b-values."""
print(f"\nGenerating mock data: {num_volumes} volumes of size ({D}, {H}, {W})...")
# From paper: 7 b-values + b=0, with b>0 in 3 directions
# 1*b=0 + 7*3 = 22 volumes
b_values = [0] + [10]*3 + [50]*3 + [80]*3 + [200]*3 + [400]*3 + [600]*3 + [1000]*3
b_values = b_values[:num_volumes] # Ensure list matches num_volumes
dMRI_volumes = []
segmentation_masks = []
# Create a base "brain"
d, h, w = np.indices((D, H, W))
brain_mask_base = ( (d - D//2)**2 / (D//2.5)**2 +
(h - H//2)**2 / (H//3)**2 +
(w - W//2)**2 / (W//3)**2 ) < 1
for i in range(num_volumes):
# Base volume with noise
volume = np.random.rand(D, H, W) * 30
mask = brain_mask_base.copy()
# Add "signal" to brain region
signal_intensity = 100 * np.exp(-b_values[i] * 0.001) # Simple signal decay
volume[mask] = signal_intensity + np.random.rand(np.sum(mask)) * 10
# --- Simulate Corruption ---
# Case 1: Corrupt Volume (Black Slice)
if i == 5:
volume[D//2, :, :] = 0 # Simulate a slice dropout
# Case 2: Corrupt Volume (Volume Change / Shift)
if i == 10:
# Shift the mask, simulating through-plane motion
mask = np.roll(brain_mask_base, shift=D//4, axis=0)
# Case 3: High Inter-Volume Motion
if i == 15:
# Shift the mask and volume
mask = np.roll(brain_mask_base, shift=H//4, axis=1)
volume = np.roll(volume, shift=H//4, axis=1)
dMRI_volumes.append(volume)
segmentation_masks.append(mask)
print("Mock data generated.")
return dMRI_volumes, segmentation_masks, b_values
# --- MAIN EXECUTION ---
if __name__ == "__main__":
# 1. Generate mock data (simulating scanner + nn-UNet)
mock_volumes, mock_masks, mock_b_values = create_mock_data(num_volumes=22)
# 2. Run the HERON analysis logic
# This is the core logic from Step 3b/3c of the paper.
# In the real pipeline, this would run inside Gadgetron.
results = run_heron_analysis(mock_volumes, mock_masks, mock_b_values)
# 3. Final Output (simulating Step 3d)
# The real pipeline would write this list to a file for the scanner.
print(f"\n(Step 3d) Volumes to re-acquire: {results['reacquisition_list']}")
