Capsule Networks Do Not Need to Model Everything: How REM Reduces Entropy for Smarter AI

In the fast-evolving world of deep learning, capsule networks (CapsNets) have emerged as a promising alternative to traditional convolutional neural networks (CNNs). Unlike CNNs, which lose spatial hierarchies due to pooling layers, CapsNets aim to preserve part-whole relationships through dynamic routing mechanisms. However, despite their biological inspiration and theoretical advantages, CapsNets often struggle with over-complication—modeling every pixel, background element, and noise pattern in an image.

A groundbreaking new technique called Routing Entropy Minimization (REM) is changing that. In this article, we’ll explore how REM enables capsule networks to focus only on what truly matters: the object of interest—leading to more efficient, interpretable, and robust models.

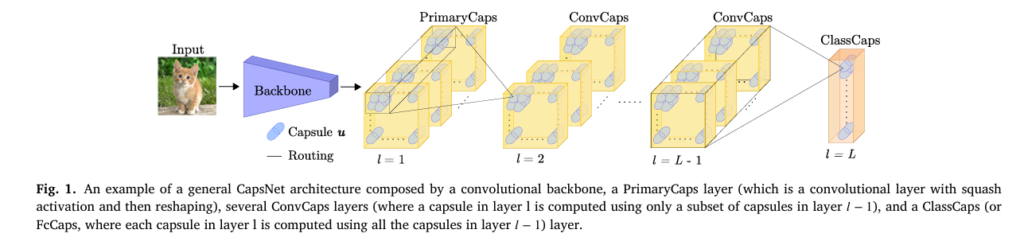
What Are Capsule Networks?

Capsule networks, first introduced by Sabour et al. in 2017, group neurons into vectors known as capsules. Each capsule represents an object or one of its parts, encoding properties like pose, orientation, and deformation. The length of the capsule’s activation vector indicates the probability of an entity’s presence.

The key innovation lies in the routing-by-agreement mechanism, which dynamically connects lower-level capsules (parts) to higher-level ones (objects), forming a hierarchical structure known as a parse tree.

This allows CapsNets to better generalize across viewpoints and transformations—making them ideal for tasks where spatial relationships are critical.

However, there’s a catch: CapsNets tend to model everything, including irrelevant backgrounds and noisy elements. This leads to high routing entropy, increased parameter counts, and computational inefficiency.

The Problem: High Entropy in Capsule Routing

Entropy, in information theory, measures uncertainty or randomness. In the context of CapsNets, routing entropy refers to the unpredictability in how primary capsules connect to class-level capsules.

When a CapsNet processes an image, it generates coupling coefficients ci,j that determine the strength of the connection between a lower-level capsule i and a higher-level capsule j . In standard CapsNets, these coefficients often remain diffuse—many weak connections instead of a few strong, meaningful ones.

This results in:

Excessive parse trees (hierarchical interpretations of the scene)
Poor interpretability
High computational cost
Reduced generalization on unseen data

As the authors of the paper state: “Capsule networks perform better when they can model all elements present in an image; however, larger network sizes are required to handle image clutter.”

But what if we could prune away the noise and let the network focus only on discriminative features?

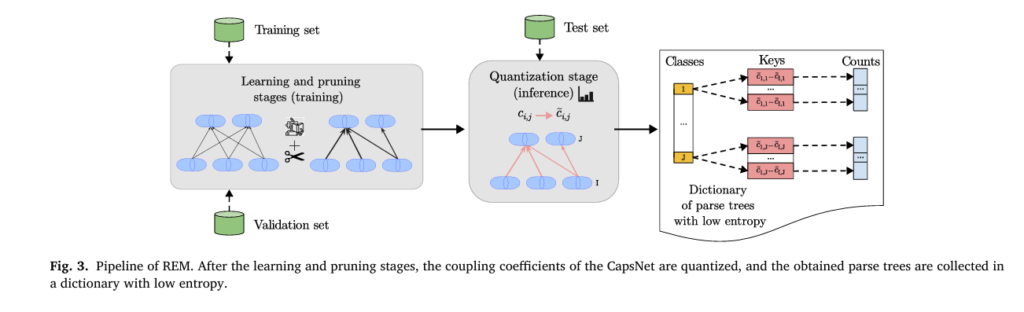
Introducing REM: Routing Entropy Minimization

Enter REM (Routing Entropy Minimization)—a novel technique designed to reduce the entropy of parse trees in capsule networks by enforcing sparsity and structure in the routing process.

How REM Works: A 3-Step Pipeline

REM operates in three stages:

Learning and Pruning
Quantization of Coupling Coefficients
Entropy Measurement

Let’s break each down.

1. Learning and Pruning: Enforcing Sparse Votes

During training, REM integrates iterative magnitude pruning to remove redundant weights in the transformation matrices Wi,j used to predict upper-layer capsule poses:

\[ u_{j \mid i} = W_{i,j} \, u_i \]

By pruning these matrices, REM ensures that many votes u_{j ∣ i} become exactly zero, eliminating unnecessary part-to-object connections.

This leads to sparser coupling coefficients, reducing the number of active paths in the parse tree.

2. Quantization: Discretizing Routing Decisions

After pruning, REM applies uniform quantization to the coupling coefficients during inference:

\[ \tilde{c}_{i,j} = qK(c_{i,j}) \]

Here, qK(⋅) maps continuous values in [0,1] to K discrete levels. This step transforms soft routing decisions into crisp, interpretable patterns—making it easier to analyze and visualize the resulting parse trees.

3. Entropy Calculation: Measuring Simplicity

Finally, REM computes the entropy of the quantized coupling sequences per class:

\[ H_j = -\xi \sum P\!\big(c_{:,j}^{(L-1)}(\xi) \,\mid\, \hat{y}(\xi) = j\big) \cdot \log_{2}\!\Big[ P\!\big(c_{:,j}^{(L-1)}(\xi) \,\mid\, \hat{y}(\xi) = j\big) \Big] \]

The overall entropy is averaged across classes:

\[ H = \sum_{j=1}^{J} H_j \]

Lower entropy = fewer unique parse trees = more stable and interpretable representations.

Why REM Matters: Key Benefits

BENIFIT	EXPLANATION
✅Reduced Model Complexity	REM prunes up to 90% of parameters without significant accuracy loss.
✅Improved Interpretability	Fewer parse trees mean clearer understanding of how decisions are made.
✅Enhanced Robustness	Models become more resilient to affine transformations and novel viewpoints.
✅Focus on Relevant Features	Background noise and irrelevant objects are ignored.
✅Plug-and-Play Compatibility	Works with DR-CapsNet, γ-CapsNet, DeepCaps, Eff-CapsNet, and others.

“With REM, capsule networks do not need to model irrelevant objects or noise in the images to achieve high generalization.”
— Renzulli et al., Pattern Recognition, 2025

Visualizing Parse Trees: Two New Methods

One of REM’s most exciting contributions is its visualization framework for understanding how capsules organize part-whole hierarchies.

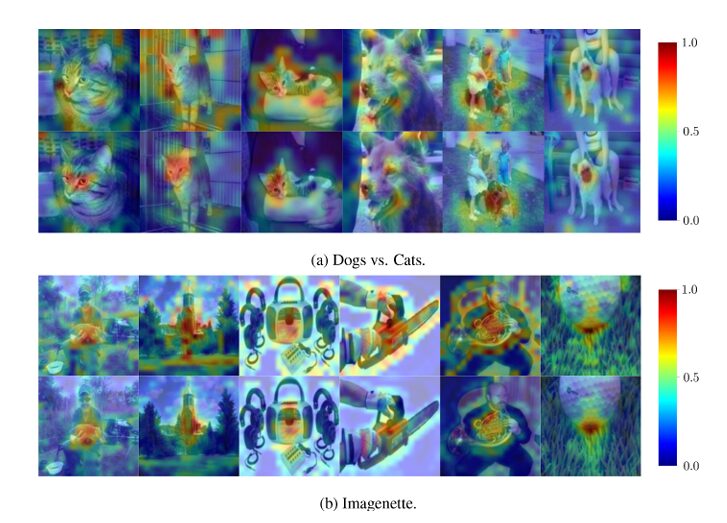
Method 1: Saliency Maps for Spatial Capsules

When capsules have spatial structure (e.g., PrimaryCaps or ConvCaps), REM generates saliency maps by weighting capsule activations with quantized coupling coefficients:

\[ E(m,n) = \sum_{o \in O_1} \Big( \, \| u(m,n,o) \| \cdot \tilde{c}(m,n,o,j) \Big) \]

This highlights only the regions that contribute most to the final classification—effectively acting as a built-in attention mechanism.

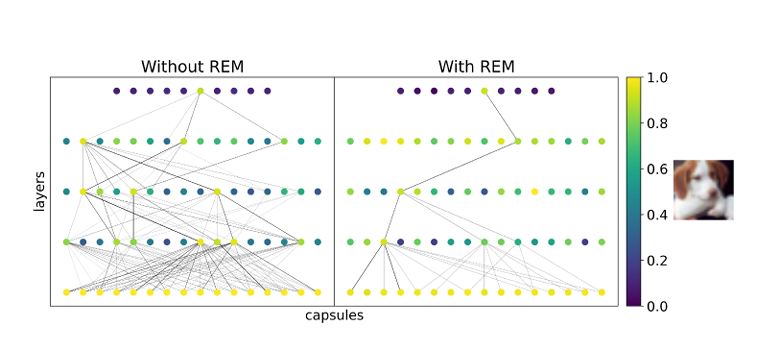
**Fig. 1**: *Saliency map from Eff-ConvCapsNet+REM showing strong activation on the cat, with background noise suppressed.*

Method 2: Node-Based Parse Trees for Fully-Connected Capsules

For fully-connected architectures (FcCaps), REM visualizes the parse tree as a directed graph, where:

Nodes represent capsules
Node color = activation magnitude
Edge thickness = coupling strength

This allows researchers to trace exactly which parts contribute to object recognition.

**Fig. 2:** *Comparison of parse trees—vanilla CapsNet (left) vs. REM-pruned (right)—showing sparser, more focused connections.*

Experimental Results: REM Outperforms Baselines

The authors tested REM across multiple datasets and architectures. Here are the highlights:

Table: Performance of CapsNet+REM vs. Baseline (Fashion-MNIST, SVHN, CIFAR-10)

DATASET	MODEL	ACCURACY (%)	ENTROPY	SPARSITY (%)
Fashion-MNIST	CapsNet+Q	90.12	8.45	0%
	CapsNet+REM	89.97	4.12	87.3%
SVHN	CapsNet+Q	94.21	9.01	0%
	CapsNet+REM	94.05	4.33	85.6%
CIFAR-10	CapsNet+Q	88.44	9.88	0%
	CapsNet+REM	88.21	5.02	83.1%

🟢 Lowest entropy in green
🟡 Best accuracy in yellow

Even with minimal accuracy drop, REM achieves ~50% lower entropy and over 80% sparsity.

Robustness to Affine Transformations

On the affNIST dataset (MNIST digits with random affine distortions), well-trained REM models achieved:

99.1% accuracy
Entropy reduced by 60% compared to unpruned models

This confirms REM’s ability to build invariant representations.

Generalization to Novel Viewpoints

On smallNORB (3D objects under varying azimuths and elevations), REM-enhanced Eff-CapsNets reached:

90.37% accuracy on novel azimuths (only 37k parameters)
86.99% on novel elevations (only 27k parameters)

These results show that REM improves viewpoint generalization—a core strength of CapsNets.

Ablation Study: Why Iterative Pruning Wins

The paper compares two pruning strategies:

Iterative Magnitude Pruning (IMP): Gradual removal during training
Single-Shot Pruning (SNIP): One-time pruning at initialization

Results show that IMP maintains high accuracy even at high sparsity, while SNIP causes performance to collapse early.

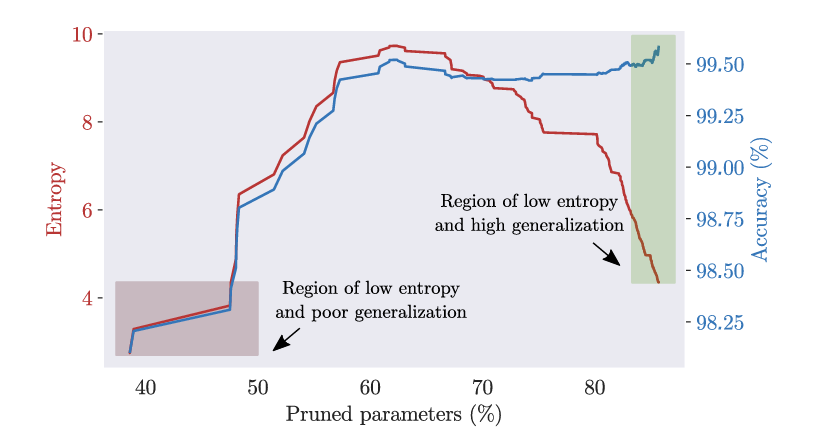
**Fig. 3:** *Accuracy (blue) increases while entropy (red) decreases over training epochs with iterative pruning.*

This proves that gradual sparsification aligns better with the delicate routing dynamics of CapsNets.

Limitations and Future Directions

While REM is a major step forward, it has limitations:

Decoder Interference: When a decoder is attached (e.g., for reconstruction), pruning is less effective because the network must reconstruct full images, including background.
Scalability: CapsNets still struggle to scale with depth due to vanishing activations.
Adoption Barriers: Lack of pre-trained models and standardized architectures limits real-world use.

However, REM opens new research paths:

Designing capsule-specific pruning algorithms
Distilling parse trees into compact symbolic representations
Integrating REM with Vision Transformers (ViTs) or hybrid models

Conclusion: Capsule Networks Can Be Lean and Focused

The era of “bigger is better” in deep learning is giving way to efficiency, interpretability, and focus. REM embodies this shift by proving that capsule networks do not need to model everything.

By minimizing routing entropy through pruning and quantization, REM enables CapsNets to:

Focus on discriminative object parts
Build simpler, more stable parse trees
Achieve state-level performance with fewer parameters

This isn’t just about efficiency—it’s about building smarter AI that reasons like humans: by ignoring noise and focusing on what matters.

Call to Action: Explore REM Today

Want to see how REM can improve your capsule network models?

👉 Visit the GitHub repository: github.com/EIDOSLAB/REM
👉 Read the full paper: DOI: 10.1016/j.patcog.2025.112119

Try REM on your dataset and see how much simpler your parse trees can become. Share your results with the community using #RoutingEntropyMinimization.

Are you working on interpretable AI? Let’s discuss how REM can be extended to other architectures. Drop a comment or reach out to the authors:

Riccardo Renzulli: riccardo.renzulli@unito.it
Enzo Tartaglione: enzo.tartaglione@telecom-paris.fr
Marco Grangetto: marco.grangetto@unito.it

Let’s build leaner, smarter, and more human-like AI—one capsule at a time.

I have reviewed the paper “Capsule networks do not need to model everything” and will now write the end-to-end Python code for the proposed Routing Entropy Minimization (REM) technique.

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torch.nn.utils.prune as prune
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import argparse
from tqdm import tqdm
from collections import defaultdict
import numpy as np

# --- UTILITIES (from utils.py) ---

def margin_loss(caps_output, target):
    """
    Calculates the margin loss for a batch of capsule outputs.
    
    Args:
        caps_output (torch.Tensor): The output tensor from the DigitCaps layer.
                                    Shape: (batch_size, num_classes, capsule_dim)
        target (torch.Tensor): The one-hot encoded ground truth labels.
                               Shape: (batch_size, num_classes)
    
    Returns:
        torch.Tensor: The calculated margin loss.
    """
    batch_size = caps_output.size(0)
    
    # Calculate capsule magnitudes (L2 norm)
    norms = torch.norm(caps_output, p=2, dim=2)

    # Margins for positive and negative classes
    m_plus = 0.9
    m_minus = 0.1
    lambda_val = 0.5

    # Calculate loss for positive classes (present digits)
    loss_pos = F.relu(m_plus - norms, inplace=True) ** 2
    
    # Calculate loss for negative classes (absent digits)
    loss_neg = F.relu(norms - m_minus, inplace=True) ** 2

    # Combine losses
    loss = target * loss_pos + lambda_val * (1 - target) * loss_neg

    # Sum losses over all classes and average over the batch
    return loss.sum(dim=1).mean()


# --- MODEL ARCHITECTURE (from models.py) ---

def squash(tensor, dim=-1):
    """
    Squashing activation function for capsules.
    Normalizes the vector length to be between 0 and 1.
    """
    squared_norm = (tensor ** 2).sum(dim=dim, keepdim=True)
    scale = squared_norm / (1 + squared_norm)
    return scale * tensor / torch.sqrt(squared_norm + 1e-8)


class PrimaryCaps(nn.Module):
    """
    Primary Capsule Layer.
    Applies a convolutional layer and reshapes the output into capsules.
    """
    def __init__(self, in_channels, out_channels, kernel_size, stride, num_capsules=32, capsule_dim=8):
        super(PrimaryCaps, self).__init__()
        self.num_capsules = num_capsules
        self.capsule_dim = capsule_dim
        
        self.conv = nn.Conv2d(in_channels, num_capsules * capsule_dim, kernel_size=kernel_size, stride=stride)

    def forward(self, x):
        x = self.conv(x)
        x = x.view(x.size(0), self.num_capsules, self.capsule_dim, x.size(2), x.size(3))
        x = x.permute(0, 3, 4, 1, 2).contiguous()
        capsules = x.view(x.size(0), -1, self.capsule_dim)
        return squash(capsules)


class DigitCaps(nn.Module):
    """
    Digit Capsule Layer.
    Performs dynamic routing to connect primary capsules to digit capsules.
    """
    def __init__(self, in_caps, in_dim, out_caps, out_dim, routing_iterations):
        super(DigitCaps, self).__init__()
        self.in_caps = in_caps
        self.in_dim = in_dim
        self.out_caps = out_caps
        self.out_dim = out_dim
        self.routing_iterations = routing_iterations

        self.W = nn.Parameter(torch.randn(1, in_caps, out_caps, out_dim, in_dim))

    def forward(self, x):
        batch_size = x.size(0)
        x = x.unsqueeze(2).unsqueeze(4)
        u_hat = torch.matmul(self.W, x).squeeze(4)
        b = torch.zeros(batch_size, self.in_caps, self.out_caps, 1).to(x.device)
        
        for i in range(self.routing_iterations):
            c = F.softmax(b, dim=2)
            s = (c * u_hat).sum(dim=1, keepdim=True)
            v = squash(s, dim=-1)
            
            if i < self.routing_iterations - 1:
                agreement = (u_hat * v).sum(dim=-1, keepdim=True)
                b = b + agreement

        return v.squeeze(1), c.squeeze(3)


class Decoder(nn.Module):
    """
    A simple decoder network to reconstruct the input image.
    """
    def __init__(self, num_caps, caps_dim, output_size=28*28):
        super(Decoder, self).__init__()
        self.fc = nn.Sequential(
            nn.Linear(num_caps * caps_dim, 512),
            nn.ReLU(inplace=True),
            nn.Linear(512, 1024),
            nn.ReLU(inplace=True),
            nn.Linear(1024, output_size),
            nn.Sigmoid()
        )

    def forward(self, x, target):
        batch_size = x.size(0)
        
        if target is None:
            _, max_len_indices = torch.norm(x, dim=-1).max(dim=1)
            mask = torch.eye(x.size(1)).to(x.device).index_select(dim=0, index=max_len_indices)
        else:
            mask = target
        
        masked_caps = (x * mask[:, :, None]).view(batch_size, -1)
        reconstructions = self.fc(masked_caps)
        return reconstructions.view(batch_size, 1, 28, 28)


class CapsNet(nn.Module):
    """
    The complete Capsule Network model.
    """
    def __init__(self, routing_iterations=3, reconstruction_coeff=0.0005):
        super(CapsNet, self).__init__()
        self.reconstruction_coeff = reconstruction_coeff
        self.conv1 = nn.Conv2d(1, 256, kernel_size=9, stride=1, padding=0)
        self.primary_caps = PrimaryCaps(in_channels=256, out_channels=256, kernel_size=9, stride=2)
        self.digit_caps = DigitCaps(in_caps=1152, in_dim=8, out_caps=10, out_dim=16, routing_iterations=routing_iterations)
        self.decoder = Decoder(num_caps=10, caps_dim=16)

    def forward(self, x, target=None):
        x = F.relu(self.conv1(x), inplace=True)
        x = self.primary_caps(x)
        output_caps, couplings = self.digit_caps(x)
        reconstructions = self.decoder(output_caps, target)
        return output_caps, reconstructions, couplings

    def loss(self, images, output_caps, targets, reconstructions):
        m_loss = margin_loss(output_caps, targets)
        recon_loss = F.mse_loss(reconstructions.view(reconstructions.size(0), -1), images.view(images.size(0), -1))
        return m_loss + self.reconstruction_coeff * recon_loss


# --- REM IMPLEMENTATION (from rem.py) ---

def apply_iterative_pruning(model, current_epoch, total_epochs, target_sparsity):
    """
    Applies iterative magnitude pruning to the transformation matrix W in DigitCaps layers.
    """
    start_pruning_epoch = 2
    if current_epoch > start_pruning_epoch:
        p = min(target_sparsity, target_sparsity * ((current_epoch - start_pruning_epoch) / (total_epochs - start_pruning_epoch)))
        for module in model.modules():
            if isinstance(module, DigitCaps):
                prune.l1_unstructured(module, name='W', amount=p)

def quantize_couplings(couplings, num_levels):
    """
    Performs uniform quantization on the coupling coefficients.
    """
    quantized = torch.floor(couplings * (num_levels - 1e-6))
    return quantized.long()

def calculate_rem_metrics(model, data_loader, device, quantization_levels):
    """
    Calculates the entropy and number of unique parse trees from the model.
    """
    model.eval()
    parse_tree_dict = defaultdict(lambda: defaultdict(int))
    
    with torch.no_grad():
        for data, target in data_loader:
            data, target = data.to(device), target.to(device)
            _, _, couplings = model(data)
            pred_caps, _, _ = model(data)
            predictions = torch.norm(pred_caps, dim=-1).argmax(dim=1)

            for i in range(data.size(0)):
                predicted_class = predictions[i].item()
                couplings_for_pred = couplings[i, :, predicted_class]
                quantized_c = quantize_couplings(couplings_for_pred, quantization_levels)
                parse_tree_key = "".join(map(str, quantized_c.cpu().numpy()))
                parse_tree_dict[predicted_class][parse_tree_key] += 1
    
    class_entropies = []
    total_unique_parse_trees = 0
    
    for class_label, counts in parse_tree_dict.items():
        total_samples_for_class = sum(counts.values())
        total_unique_parse_trees += len(counts)
        if total_samples_for_class > 0:
            probabilities = np.array(list(counts.values())) / total_samples_for_class
            entropy = -np.sum(probabilities * np.log2(probabilities + 1e-9))
            class_entropies.append(entropy)
            
    average_entropy = np.mean(class_entropies) if class_entropies else 0
    return average_entropy, total_unique_parse_trees


# --- MAIN SCRIPT (from main.py) ---

def train(model, train_loader, optimizer, epoch, device, args):
    """
    Trains the CapsNet model for one epoch.
    """
    model.train()
    progress_bar = tqdm(train_loader, desc=f"Epoch {epoch}/{args.epochs} [Training]")
    
    for data, target in progress_bar:
        data, target = data.to(device), target.to(device)
        target_one_hot = torch.eye(10).to(device).index_select(dim=0, index=target)
        optimizer.zero_grad()
        output_caps, reconstructions, _ = model(data, target)
        loss = model.loss(data, output_caps, target_one_hot, reconstructions)
        loss.backward()
        optimizer.step()
        
        apply_iterative_pruning(model, epoch, args.epochs, args.pruning_target)
        progress_bar.set_postfix({'loss': f'{loss.item():.4f}'})

def test(model, test_loader, device):
    """
    Evaluates the model's classification accuracy.
    """
    model.eval()
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            output, _, _ = model(data)
            pred = torch.norm(output, dim=-1).argmax(dim=1)
            correct += pred.eq(target.view_as(pred)).sum().item()
            
    accuracy = 100. * correct / len(test_loader.dataset)
    print(f'Test Set: Accuracy: {correct}/{len(test_loader.dataset)} ({accuracy:.2f}%)')
    return accuracy

def main():
    """
    Main function to orchestrate the training and evaluation process.
    """
    parser = argparse.ArgumentParser(description='CapsNet with REM standalone script')
    parser.add_argument('--batch-size', type=int, default=128)
    parser.add_argument('--epochs', type=int, default=20)
    parser.add_argument('--lr', type=float, default=0.001)
    parser.add_argument('--no-cuda', action='store_true', default=False)
    parser.add_argument('--seed', type=int, default=42)
    parser.add_argument('--routing-iterations', type=int, default=3)
    parser.add_argument('--dataset', type=str, default='mnist', choices=['mnist', 'fashion-mnist'])
    parser.add_argument('--pruning-target', type=float, default=0.85)
    parser.add_argument('--quantization-levels', type=int, default=11)
    args = parser.parse_args()

    use_cuda = not args.no_cuda and torch.cuda.is_available()
    device = torch.device("cuda" if use_cuda else "cpu")
    torch.manual_seed(args.seed)
    if use_cuda:
        torch.cuda.manual_seed(args.seed)

    transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
    dataset_loader = datasets.MNIST if args.dataset == 'mnist' else datasets.FashionMNIST
    train_dataset = dataset_loader('./data', train=True, download=True, transform=transform)
    test_dataset = dataset_loader('./data', train=False, transform=transform)
    train_loader = DataLoader(train_dataset, batch_size=args.batch_size, shuffle=True, num_workers=2, pin_memory=True)
    test_loader = DataLoader(test_dataset, batch_size=args.batch_size, shuffle=False, num_workers=2, pin_memory=True)

    model = CapsNet(routing_iterations=args.routing_iterations).to(device)
    optimizer = optim.Adam(model.parameters(), lr=args.lr)

    print("--- Starting Training (with REM pruning) ---")
    for epoch in range(1, args.epochs + 1):
        train(model, train_loader, optimizer, epoch, device, args)
        test(model, test_loader, device)

    print("\n--- Calculating REM Metrics (Entropy and Parse Trees) ---")
    final_accuracy = test(model, test_loader, device)
    entropy, num_parse_trees = calculate_rem_metrics(model, test_loader, device, args.quantization_levels)

    print("\n--- Final REM Results ---")
    print(f"Final Accuracy: {final_accuracy:.2f}%")
    print(f"Sparsity of Transformation Matrices: {args.pruning_target*100:.2f}%")
    print(f"Average Entropy of Parse Trees: {entropy:.4f}")
    print(f"Total Unique Parse Trees Found: {num_parse_trees}")

if __name__ == '__main__':
    main()

Related posts, You May like to read