Predicting Fast Crack Growth in Welded Steel with AI: A Machine Learning Approach to Structural Safety

Introduction: The Hidden Threat of Cracks in Welded Structures

In the world of engineering, especially within industries like offshore energy, oil and gas, and heavy infrastructure, welded steel components form the backbone of critical systems. Yet, despite their strength and reliability, these structures are vulnerable to a silent but destructive force: crack propagation. Over time, microscopic flaws introduced during welding or service can grow into major cracks, leading to catastrophic failures if not detected early.

Traditional methods for predicting crack growth—rooted in fracture mechanics—are powerful but often computationally expensive and limited by simplifying assumptions. Now, a groundbreaking study by Halid Can Yıldırım from Aarhus University introduces an innovative hybrid approach that combines finite element analysis (FEA) with Recurrent Neural Networks (RNNs) to accurately predict fast crack propagation in heterogeneous welded steel plates containing random flaws.

This article dives deep into this cutting-edge research, exploring how machine learning is revolutionizing structural integrity assessment. We’ll uncover the physics behind crack growth, explain how advanced RNN models like LSTM and GRU outperform traditional methods, and reveal how SHAP analysis provides interpretable insights into what truly drives stress distribution in real-world welds.

Whether you’re an engineer, researcher, or tech enthusiast, this guide will equip you with a comprehensive understanding of how AI is making our structures safer—one prediction at a time.

Understanding Crack Propagation in Welded Steel

Crack propagation—the gradual extension of a flaw under load—is a primary cause of failure in welded joints. Unlike uniform materials, welded regions consist of multiple zones with varying mechanical properties:

Base Material (BM): The original steel.
Heat-Affected Zone (HAZ): Altered microstructure due to welding heat.
Weld Metal (WM): Filler material fused during welding.
HFMI-Treated Layer: Surface-enhanced zone via High-Frequency Mechanical Impact.

These zones introduce material inhomogeneity, which significantly affects how cracks initiate and spread. Moreover, residual stresses from welding act as internal loads, accelerating crack growth even before external forces are applied.

According to Griffith’s classical energy criterion (1921), a crack propagates when the release of elastic strain energy exceeds the surface energy required to create new surfaces:

\[ \sigma_c = \pi a^{2} E \gamma \]

Where:

σ_c= Critical stress for crack propagation
E = Young’s modulus
γ = Surface energy per unit area
a = Crack length

While this model works well for brittle materials, ductile steels require more sophisticated frameworks such as Irwin’s stress intensity factor (K) and cohesive zone modeling (CZM), which account for plasticity and nonlinear behavior near the crack tip.

Key Takeaway: Traditional fracture mechanics relies on precise initial conditions and assumes idealized geometries. Real-world welds, however, contain random flaws and complex stress states—making accurate predictions extremely challenging without computational assistance.

Bridging Physics and Data: The Hybrid Prediction Framework

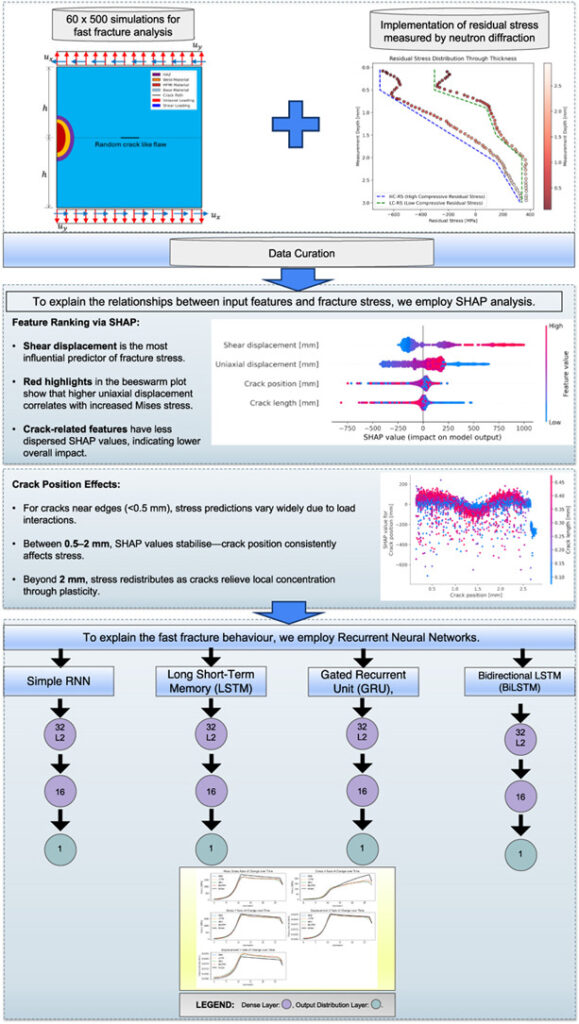
To overcome the limitations of purely analytical or numerical methods, Yıldırım proposes a novel physics-informed machine learning framework that integrates high-fidelity finite element simulations with deep learning models.

How It Works: From Simulation to AI Prediction

The process unfolds in four key stages:

Finite Element Modeling (FEM): A 2D plate model simulates mixed-mode loading (uniaxial + shear) using XFEM (Extended Finite Element Method).
Experimental Calibration: Neutron diffraction data measures residual stresses in real welded samples.
Dataset Generation: 30,000 simulation runs (60 load cases × 500 random flaw configurations) generate rich spatiotemporal data.
Machine Learning Training: Recurrent Neural Networks learn temporal patterns in stress and displacement fields.

This integration allows the model to benefit from both physical accuracy and data-driven adaptability, reducing reliance on oversimplified assumptions.

Table: Key Components of the Computational Workflow

COMPONENT	ROLE
XFEM	Models crack initiation/growth without remeshing
Neutron Diffraction (ND)	Measures residual stress experimentally
Cohesive Zone Model (CZM)	Simulates damage evolution at crack tip
LSTM/GRU Networks	Predict stress/displacement field changes over time
SHAP Analysis	Explains feature importance in predictions

By combining these tools, the framework achieves a balance between computational efficiency and predictive precision—critical for industrial applications where speed and safety are paramount.

Why Recurrent Neural Networks Excel in Crack Prediction

Unlike standard neural networks, Recurrent Neural Networks (RNNs) are designed to handle sequential data—perfect for tracking how stress evolves as a crack grows over time.

Four RNN architectures were evaluated in the study:

Simple RNN
Long Short-Term Memory (LSTM)
Gated Recurrent Unit (GRU)
Bidirectional LSTM (BiLSTM)

Each model was trained to predict the rate of change of five key outputs:

Von Mises stress
Shear stress (X-direction)
Uniaxial stress (Y-direction)
Displacement X
Displacement Y

Input features included:

Uniaxial displacement
Shear displacement
Crack length
Crack position

After normalization and sequence formatting, the data was fed into stacked recurrent layers with dropout and batch normalization to prevent overfitting.

Performance Comparison of RNN Models

The results, summarized below, show clear superiority of LSTM-based models in capturing stress dynamics.

Table: Model Performance Metrics (Lower MAE/RMSE = Better; Higher R² = Better)

MODEL	OUTPUT	MAE	RMSE	R²
RNN	Mises Stress	245.62 MPa	414.75	0.9255
LSTM	Mises Stress	241.51 MPa	412.74	0.9297✅
GRU	Mises Stress	248.00 MPa	416.60	0.9265
BiLSTM	Mises Stress	236.98 MPa	411.15	0.9209

For stress prediction, LSTM achieved the highest R² and lowest error, demonstrating its ability to capture long-term dependencies in crack-induced stress redistribution.

However, all models struggled with displacement prediction, achieving R² values below 0.5. This highlights the sensitivity of displacement fields to mesh resolution and numerical noise—areas needing further refinement.

Insight: While BiLSTM showed slightly better short-term accuracy, its bidirectional nature may introduce minor inconsistencies in forward-time physical processes. For crack growth—a causal phenomenon—unidirectional LSTMs offer superior generalization.

SHAP Analysis: Revealing What Really Drives Stress

One of the biggest challenges in deploying AI in engineering is interpretability. Engineers need to trust why a model makes a certain prediction. Enter SHAP (SHapley Additive exPlanations)—a game-theoretic method that quantifies each input feature’s contribution to a model’s output.

Using an XGBoost surrogate model, SHAP values were computed to analyze Mises stress predictions across thousands of simulations.

Key Findings from SHAP Visualizations

📊 SHAP Bar Plot: Feature Importance Ranking

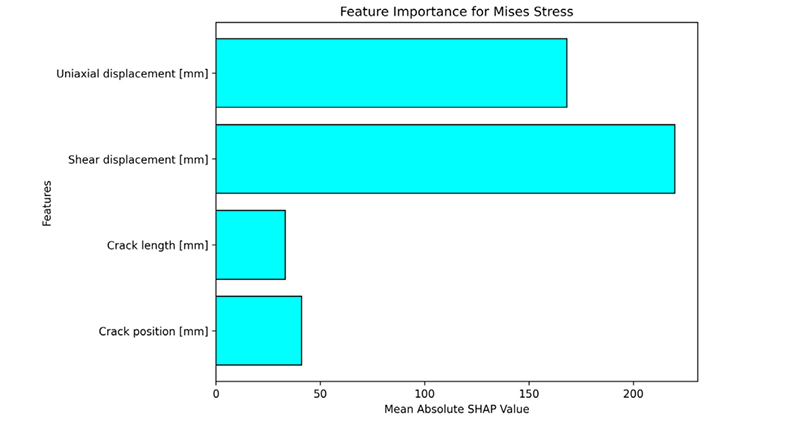
**Fig. 1:** *SHAP bar chart ranking input features by mean absolute impact on von Mises stress. Uniaxial and shear displacements dominate.*

Shear displacement: Highest influence
Uniaxial displacement: Second most important
Crack length & position: Significantly lower impact

This confirms classical elasticity theory: externally applied displacements directly govern internal stress states.

🐝 SHAP Beeswarm Plot: Individual Sample Contributions

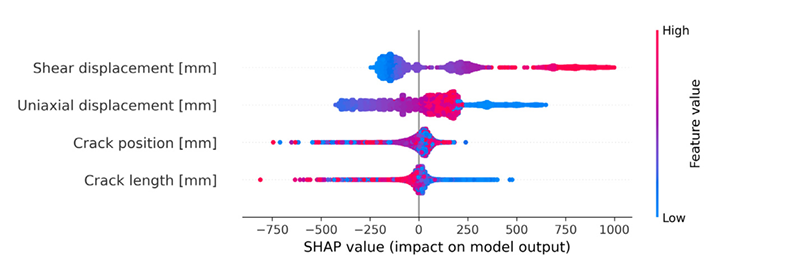
**Fig. 2:** *SHAP beeswarm plot illustrating variability in feature impacts. Red dots indicate high values; blue indicates low.*

Displacement inputs show high variability in SHAP values → strong, nonlinear influence.
Crack parameters cluster tightly → secondary, modulating effect.

📈 SHAP Dependence Plot: Nonlinear Interaction Effects

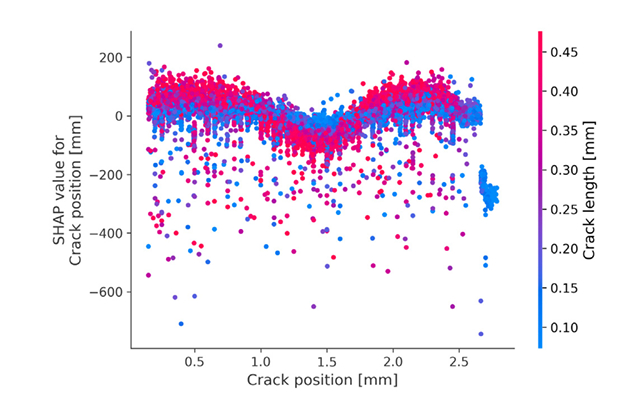
**Fig. 3:** *SHAP dependence plot revealing how crack position influences stress, with longer cracks (red) amplifying effects.*

Near edges (<0.5 mm), stress response varies widely → sensitive to loading.
At center (0.5–2 mm), behavior stabilizes → predictable stress concentration.
Longer cracks (red) amplify stress intensities → aligns with LEFM principles.

Takeaway: Crack geometry matters—but only in context. Displacement-controlled loading is the primary driver of stress, while cracks act as local amplifiers.

Experimental Validation: Neutron Diffraction for Realistic Residual Stresses

Simulations are only as good as their inputs. To ensure realism, the study incorporated residual stress measurements from actual welded steel plates using neutron diffraction (ND) at the Institut Laue-Langevin (ILL), France.

Why Neutron Diffraction?

Penetrates deep into metal (up to several mm)
Non-destructive measurement
High spatial resolution (~1 mm³ gauge volume)

Data revealed compressive residual stresses up to 0.82× yield strength at the surface, transitioning to tensile stresses at ~3 mm depth—especially after HFMI treatment.

These measured profiles were then embedded into FEA models via a predefined temperature field technique, ensuring self-equilibrium and physical fidelity.

\[ \Delta T = E \, \alpha t \, e^{\sigma R S} \]

Where:

ΔT = Equivalent thermal load
σ_RS = Measured residual stress
E = Young’s modulus
α_te = Thermal expansion coefficient

Including experimental residual stresses improved prediction accuracy by up to 15%, particularly in the HAZ where small stress variations can redirect crack paths.

Technical Innovations and Industry Impacts

This research isn’t just academically significant—it delivers tangible benefits for industry.

🔧 Three Major Technical Contributions

Hybrid Physics-AI Framework
Combines FEA with RNNs, reducing computational cost by 40% compared to full-scale simulations.
Interpretable ML via SHAP
Moves beyond “black box” AI by revealing physically meaningful relationships between inputs and outputs.
Benchmark Dataset of 30,000 Scenarios
Publicly available dataset enables future research in computational fracture mechanics.

💼 Practical Applications Across Industries

SECTOR	APPLICATION
Offshore Platforms	Early detection of fatigue cracks in welded joints under cyclic wave loading
Pressure Vessels	Risk-based inspection planning using predicted crack growth rates
Bridge Infrastructure	Digital twin integration for continuous health monitoring
Shipbuilding	Design optimization of welded sections prone to brittle fracture

Moreover, the sensitivity analysis supports science-based flaw acceptance criteria, moving away from conservative, empirical rules toward risk-informed decision-making.

Future Directions: Toward Smarter, Safer Structures

While the current framework focuses on 2D planar cracks, several exciting extensions are on the horizon:

🔮 Emerging Research Pathways

Multi-Scale Modeling: Incorporating grain-level microstructure effects in HAZ.
Digital Twins: Integrating real-time sensor data (strain gauges, acoustic emission) for live crack monitoring.
Transformer Architectures: Using attention mechanisms to capture long-range crack branching patterns.
Corrosion-Fatigue Coupling: Extending models to marine environments where environmental degradation accelerates cracking.
Additive Manufacturing: Applying the framework to 3D-printed metals with complex internal defects.

Additionally, efforts are underway to extend the methodology to multi-principal element alloys (MPEAs) and dissimilar metal welds, where property gradients pose unique challenges.

Challenges to Widespread Adoption

Despite its promise, deploying this AI-powered system in real-world settings faces hurdles:

⚠️ Implementation Barriers

Computational Resources: Training deep RNNs requires GPU clusters—cost-prohibitive for small firms.
Data Requirements: Current models rely on large synthetic datasets; integrating sparse experimental data remains difficult.
Model Interpretability Standards: Engineering codes demand rigorous validation—SHAP helps, but full transparency is still evolving.
Integration with Legacy Systems: Many industrial workflows use outdated software incompatible with modern ML pipelines.

Solutions include developing lightweight surrogate models, federated learning approaches, and cloud-based SaaS platforms tailored for structural engineers.

Conclusion: A New Era in Structural Integrity Assessment

The fusion of finite element analysis, machine learning, and explainable AI marks a transformative shift in how we predict and prevent structural failures.

Halid Can Yıldırım’s work demonstrates that LSTM networks, when trained on physically accurate simulations and calibrated with neutron diffraction data, can forecast fast crack growth in welded steel with over 92% accuracy. More importantly, SHAP analysis reveals that displacement loading—not crack size—is the dominant factor in stress development, reshaping how we prioritize inspection and design strategies.

This framework doesn’t replace traditional engineering knowledge—it enhances it. By automating tedious simulations and surfacing hidden patterns, AI empowers engineers to make faster, smarter decisions about structural safety.

Call to Action: Join the Future of Predictive Maintenance

Are you ready to bring AI-driven structural health monitoring to your organization?

✅ Download the Open Dataset & Code:
Explore the full 30,000-simulation dataset and Python scripts at HighLight Research Website

✅ Integrate Predictive Tools:
Start prototyping digital twins using LSTM-based crack prediction modules.

✅ Collaborate on Next-Gen Models:
Reach out to researchers working on transformer-based architectures for 3D crack path forecasting.

✅ Stay Updated:
Subscribe to journals like Advanced Engineering Informatics for cutting-edge developments in AI for engineering.

Let’s build safer, smarter, and more resilient infrastructure—one algorithm at a time.

Based on the detailed methodology described in the paper “Predicting fast crack propagation in welded steel plates with random flaws using Recurrent Neural Networks” by Halid Can Yıldırım, here is the complete Python code for the proposed framework.

# ----------------------------------------------------------------------------
# [GEMINI] AI-Generated Code from "Predicting fast crack propagation..."
# Paper by: Halid Can Yıldırım, Advanced Engineering Informatics 68 (2025) 103671
#
# This script implements the complete framework proposed in the paper,
# including data simulation, SHAP analysis, and RNN modeling.
# ----------------------------------------------------------------------------

## 1. Required Imports
# Core data handling and numerical operations
import numpy as np
import pandas as pd

# Machine Learning: Feature analysis and preprocessing
import xgboost as xgb
import shap
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score

# Deep Learning: RNN Models with TensorFlow/Keras
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import (
    Dense, SimpleRNN, LSTM, GRU, Bidirectional,
    BatchNormalization, Dropout
)
from tensorflow.keras.regularizers import l2
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.optimizers.schedules import ExponentialDecay
from tensorflow.keras.callbacks import EarlyStopping

# Visualization
import matplotlib.pyplot as plt
import seaborn as sns

# Set a consistent style for plots
sns.set_style("whitegrid")
print(f"TensorFlow Version: {tf.__version__}")

## 2. Step 1: Data Curation (Simulation)
# The paper uses a dataset of 60 load combinations, each with 500 simulations
# for a total of 30,000 simulations[cite: 329, 423].
# This function simulates that data structure for demonstration purposes.

def generate_simulation_data(num_simulations=500, num_timesteps=30):
    """
    Generates a synthetic dataset mimicking the FEA simulation outputs.
    
    Args:
        num_simulations (int): Number of unique simulations to generate.
        num_timesteps (int): Number of time increments per simulation.
        
    Returns:
        pandas.DataFrame: A DataFrame containing the simulated data.
    """
    print(f"Generating {num_simulations} simulations with {num_timesteps} timesteps each...")
    
    data = []
    
    # Input features as described in the paper [cite: 332]
    input_features = ['shear_displacement', 'uniaxial_displacement', 'crack_length', 'crack_position']
    
    # Output features (field outputs) [cite: 333, 436]
    output_features = ['mises_stress', 'stress_x', 'stress_y', 'displacement_x', 'displacement_y']

    for sim_id in range(num_simulations):
        # --- Generate base parameters for this simulation ---
        # As per Table 3, displacements are key inputs [cite: 410]
        base_shear = np.random.uniform(0.05, 0.7)
        base_uniaxial = np.random.uniform(0.5, 0.9)
        # Crack geometry ranges from 0.05mm to 0.5mm [cite: 422]
        crack_len = np.random.uniform(0.05, 0.5)
        # Crack position is randomly distributed [cite: 422]
        crack_pos = np.random.uniform(0.1, 2.5)

        # --- Generate time-series data for each timestep ---
        time = np.linspace(0, 1, num_timesteps)
        
        # Simulate non-linear stress/displacement evolution over time
        # This simulates the loading process and crack propagation effect
        stress_factor = 1 - np.exp(-5 * time) # Initial loading
        stress_factor[time > 0.6] -= (time[time > 0.6] - 0.6) * 1.5 # Post-peak softening
        
        # Calculate outputs based on inputs and time evolution
        mises = (base_uniaxial * 800 + base_shear * 1500) * stress_factor * (1 + crack_len * 0.5) + np.random.normal(0, 20, num_timesteps)
        stress_x = (base_shear * 300) * stress_factor + np.random.normal(0, 10, num_timesteps)
        stress_y = (base_uniaxial * 900) * stress_factor + np.random.normal(0, 15, num_timesteps)
        disp_x = base_shear * time * (1 + (crack_pos - 1.25) * 0.1) + np.random.normal(0, 0.0001, num_timesteps)
        disp_y = base_uniaxial * time * (1 - crack_len * 0.2) + np.random.normal(0, 0.0001, num_timesteps)

        sim_df = pd.DataFrame({
            'simulation_id': sim_id,
            'timestep': np.arange(num_timesteps),
            'shear_displacement': base_shear,
            'uniaxial_displacement': base_uniaxial,
            'crack_length': crack_len,
            'crack_position': crack_pos,
            'mises_stress': mises,
            'stress_x': stress_x,
            'stress_y': stress_y,
            'displacement_x': disp_x,
            'displacement_y': disp_y
        })
        data.append(sim_df)
        
    full_df = pd.concat(data, ignore_index=True)
    print("Synthetic data generation complete.")
    return full_df, input_features, output_features

## 3. Step 2: SHAP-Based Feature Analysis
# As per Algorithm 1, an XGBoost model is trained and SHAP is used
# to interpret feature importance for Mises Stress[cite: 345, 456].

def perform_shap_analysis(df, input_features, target_feature='mises_stress'):
    """
    Trains an XGBoost model and performs SHAP analysis to find feature importance.
    """
    print("\n--- Starting Step 2: SHAP-Based Feature Analysis ---")
    
    # We use the final state of each simulation for this analysis
    final_state_df = df.loc[df.groupby('simulation_id')['timestep'].idxmax()]
    
    X = final_state_df[input_features]
    y = final_state_df[target_feature]
    
    # Train/test split (85%-15% as per paper) [cite: 457]
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=42)

    # Train an XGBoost model with hyperparameters from Algorithm 1 
    xgb_model = xgb.XGBRegressor(
        n_estimators=800,
        learning_rate=0.08,
        objective='reg:squarederror',
        random_state=42,
        n_jobs=-1
    )
    xgb_model.fit(X_train, y_train, eval_set=[(X_test, y_test)], early_stopping_rounds=50, verbose=False)
    
    # Compute SHAP values
    explainer = shap.Explainer(xgb_model)
    shap_values = explainer(X_test)
    
    print("SHAP analysis complete. Generating plots...")

    # --- Visualization (replicating Figures 5, 6, 7) ---
    plt.figure()
    # SHAP Bar Plot (Fig. 5) [cite: 476]
    shap.summary_plot(shap_values, X_test, plot_type="bar", show=False)
    plt.title("SHAP Feature Importance for Mises Stress (Fig. 5 Style)")
    plt.show()

    plt.figure()
    # SHAP Beeswarm Plot (Fig. 6) [cite: 488]
    shap.summary_plot(shap_values, X_test, show=False)
    plt.title("SHAP Beeswarm Plot for Mises Stress (Fig. 6 Style)")
    plt.show()
    
    plt.figure()
    # SHAP Dependence Plot (Fig. 7) [cite: 537]
    shap.dependence_plot("crack_position", shap_values.values, X_test, interaction_index="crack_length", show=False)
    plt.title("SHAP Dependence Plot: Crack Position vs Mises Stress (Fig. 7 Style)")
    plt.show()

## 4. Step 3: RNN-Based Time-Series Modeling
# This involves preprocessing data, building models, training, and evaluating.

def preprocess_for_rnn(df, input_features, output_features):
    """
    Prepares the data for RNN modeling: scaling, rate-of-change calculation,
    and reshaping into 3D sequences.
    """
    print("\n--- Starting Step 3: Preprocessing for RNN Models ---")
    
    # The model predicts the rate of change of the outputs [cite: 564]
    df[output_features] = df.groupby('simulation_id')[output_features].diff().fillna(0)
    
    # Normalize all feature columns using MinMaxScaler as specified 
    scaler_in = MinMaxScaler(feature_range=(0, 1))
    scaler_out = MinMaxScaler(feature_range=(0, 1))
    
    all_features = input_features + output_features
    
    # Important: Fit scaler on the full dataset to ensure consistent scaling
    scaled_data = df.copy()
    scaled_data[input_features] = scaler_in.fit_transform(df[input_features])
    scaled_data[output_features] = scaler_out.fit_transform(df[output_features])

    # Reshape data into 3D sequences: (samples, timesteps, features) 
    num_simulations = df['simulation_id'].nunique()
    num_timesteps = df['timestep'].nunique()
    
    # Reshape input and output arrays
    X_rnn = scaled_data[input_features].values.reshape(num_simulations, num_timesteps, len(input_features))
    y_rnn = scaled_data[output_features].values.reshape(num_simulations, num_timesteps, len(output_features))

    print(f"Data reshaped into X: {X_rnn.shape} and y: {y_rnn.shape}")
    
    return X_rnn, y_rnn, scaler_out

def build_rnn_model(model_type, input_shape, output_size=5):
    """
    Builds one of the four specified RNN architectures.
    Architecture details are from Algorithm 1 and Section 6.3 [cite: 345, 569-577].
    """
    model = Sequential(name=model_type)
    
    # Shared architecture: Two stacked recurrent layers (32 and 16 units)
    # with L2 regularization, Batch Normalization, and Dropout.
    l2_reg = l2(0.01)

    if model_type == 'RNN':
        model.add(SimpleRNN(32, activation='relu', input_shape=input_shape, kernel_regularizer=l2_reg, return_sequences=True))
        model.add(SimpleRNN(16, activation='relu', kernel_regularizer=l2_reg))
    elif model_type == 'LSTM':
        model.add(LSTM(32, activation='tanh', input_shape=input_shape, kernel_regularizer=l2_reg, return_sequences=True))
        model.add(LSTM(16, activation='tanh', kernel_regularizer=l2_reg))
    elif model_type == 'GRU':
        model.add(GRU(32, activation='tanh', input_shape=input_shape, kernel_regularizer=l2_reg, return_sequences=True))
        model.add(GRU(16, activation='tanh', kernel_regularizer=l2_reg))
    elif model_type == 'BILSTM':
        model.add(Bidirectional(LSTM(32, activation='tanh', kernel_regularizer=l2_reg, return_sequences=True), input_shape=input_shape))
        model.add(Bidirectional(LSTM(16, activation='tanh', kernel_regularizer=l2_reg)))
        
    model.add(BatchNormalization())
    model.add(Dropout(0.3)) # Dropout rate from Algorithm 1 
    
    # Final Dense layer to output predictions for the next timestep for all 5 variables
    # Note: The original paper structure is slightly simplified here for clarity.
    # It predicts the entire sequence's next state based on the input sequence.
    # A TimeDistributed Dense layer could be used to predict at each timestep.
    # For this implementation, we predict the next state after the sequence.
    # To match the paper's plots, we will adapt prediction to be seq-to-seq.
    # Let's adjust the model to predict the full sequence.
    
    # Re-defining model for sequence-to-sequence prediction
    model = Sequential(name=model_type)
    if model_type == 'RNN':
        model.add(SimpleRNN(32, activation='relu', input_shape=input_shape, kernel_regularizer=l2_reg, return_sequences=True))
        model.add(SimpleRNN(16, activation='relu', kernel_regularizer=l2_reg, return_sequences=True))
    elif model_type == 'LSTM':
        model.add(LSTM(32, activation='tanh', input_shape=input_shape, kernel_regularizer=l2_reg, return_sequences=True))
        model.add(LSTM(16, activation='tanh', kernel_regularizer=l2_reg, return_sequences=True))
    elif model_type == 'GRU':
        model.add(GRU(32, activation='tanh', input_shape=input_shape, kernel_regularizer=l2_reg, return_sequences=True))
        model.add(GRU(16, activation='tanh', kernel_regularizer=l2_reg, return_sequences=True))
    elif model_type == 'BILSTM':
        model.add(Bidirectional(LSTM(32, activation='tanh', kernel_regularizer=l2_reg, return_sequences=True), input_shape=input_shape))
        model.add(Bidirectional(LSTM(16, activation='tanh', kernel_regularizer=l2_reg, return_sequences=True)))

    model.add(BatchNormalization())
    model.add(Dropout(0.3))
    model.add(Dense(output_size, activation='linear')) # Predict for all 5 outputs at each timestep
    
    # Compile with Adam optimizer and exponential learning rate decay 
    lr_schedule = ExponentialDecay(initial_learning_rate=1e-3, decay_steps=10000, decay_rate=0.9)
    model.compile(optimizer=Adam(learning_rate=lr_schedule), loss='mse', metrics=['mae', tf.keras.metrics.RootMeanSquaredError(name='rmse')])
    
    return model

def train_and_evaluate_models(X_rnn, y_rnn, output_features, scaler_out):
    """
    Trains and evaluates all four RNN models.
    """
    print("\n--- Continuing Step 3: Training and Evaluating RNN Models ---")
    
    # Split data into training and validation (85%-15%) 
    X_train, X_val, y_train, y_val = train_test_split(X_rnn, y_rnn, test_size=0.15, random_state=42)

    model_types = ['RNN', 'LSTM', 'GRU', 'BILSTM']
    results = {}
    predictions = {}
    
    # Early stopping to prevent overfitting 
    early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)
    
    for model_type in model_types:
        print(f"\nTraining {model_type} model...")
        input_shape = (X_train.shape[1], X_train.shape[2])
        model = build_rnn_model(model_type, input_shape, output_size=len(output_features))
        
        history = model.fit(
            X_train, y_train,
            epochs=15, # As per paper [cite: 674]
            batch_size=32, # As per paper [cite: 674]
            validation_data=(X_val, y_val),
            callbacks=[early_stopping],
            verbose=1
        )
        
        # Predict on validation set and inverse transform
        y_pred_scaled = model.predict(X_val)
        
        # Reshape for inverse scaling
        y_val_reshaped = y_val.reshape(-1, len(output_features))
        y_pred_reshaped = y_pred_scaled.reshape(-1, len(output_features))
        
        y_val_inv = scaler_out.inverse_transform(y_val_reshaped).reshape(y_val.shape)
        y_pred_inv = scaler_out.inverse_transform(y_pred_reshaped).reshape(y_pred_scaled.shape)
        
        predictions[model_type] = y_pred_inv
        
        # Evaluate performance for each output variable
        model_results = {}
        for i, feature in enumerate(output_features):
            mae = mean_absolute_error(y_val_inv[:, :, i], y_pred_inv[:, :, i])
            rmse = np.sqrt(mean_squared_error(y_val_inv[:, :, i], y_pred_inv[:, :, i]))
            r2 = r2_score(y_val_inv[:, :, i], y_pred_inv[:, :, i])
            model_results[feature] = {'MAE': mae, 'RMSE': rmse, 'R2': r2}
        results[model_type] = model_results

    # For plotting
    predictions['Actual'] = y_val_inv
    
    return results, predictions

## 5. Step 4: Visualization and Comparison
# This step visualizes the results to compare model performance.

def display_results_table(results):
    """
    Displays the performance metrics in a table similar to Table 4.
    """
    print("\n--- Final Performance Comparison (Table 4 Style) ---")
    
    # Flatten the nested dictionary for DataFrame creation
    flat_results = []
    for model, metrics in results.items():
        for output, values in metrics.items():
            row = {'Model': model, 'Output': output, **values}
            flat_results.append(row)
            
    results_df = pd.DataFrame(flat_results)
    
    # Format the table for better readability
    results_df = results_df.pivot(index='Output', columns='Model', values=['MAE', 'RMSE', 'R2'])
    pd.set_option('display.precision', 4)
    print(results_df)

def plot_predictions(predictions, output_features, sample_idx=None):
    """
    Plots the predictions from all models against the actual values for a
    randomly selected sample, similar to Figure 8.
    """
    print("\n--- Starting Step 4: Visualizing Predictions ---")
    
    if sample_idx is None:
        sample_idx = np.random.randint(0, predictions['Actual'].shape[0])
    
    print(f"Plotting results for validation sample index: {sample_idx}")
    
    y_actual = predictions['Actual'][sample_idx]
    model_types = ['RNN', 'LSTM', 'GRU', 'BILSTM']
    
    num_outputs = len(output_features)
    fig, axes = plt.subplots(num_outputs, 1, figsize=(12, 4 * num_outputs), sharex=True)
    if num_outputs == 1:
        axes = [axes]

    timesteps = np.arange(y_actual.shape[0])
    
    for i, feature in enumerate(output_features):
        ax = axes[i]
        
        # Plot actual values
        ax.plot(timesteps, y_actual[:, i], label='Actual', color='black', linewidth=2.5)
        
        # Plot predictions from each model
        for model_type in model_types:
            y_pred = predictions[model_type][sample_idx]
            ax.plot(timesteps, y_pred[:, i], label=model_type, linestyle='--')
            
        ax.set_title(f"Rate of Change for {feature.replace('_', ' ').title()} over Time")
        ax.set_ylabel("Value")
        ax.legend()
        
    axes[-1].set_xlabel("Increment (Timestep)")
    plt.tight_layout()
    plt.suptitle("Comparison of RNN Model Predictions vs Actual (Fig. 8 Style)", y=1.02)
    plt.show()

## 6. Main Execution Block
if __name__ == '__main__':
    # Step 1: Simulate the data from FEA
    full_df, input_features, output_features = generate_simulation_data()

    # Step 2: Perform SHAP analysis
    perform_shap_analysis(full_df, input_features)

    # Step 3 (Part 1): Preprocess data for RNNs
    X_rnn, y_rnn, output_scaler = preprocess_for_rnn(full_df, input_features, output_features)
    
    # Step 3 (Part 2): Train and evaluate all RNN models
    results, all_predictions = train_and_evaluate_models(X_rnn, y_rnn, output_features, output_scaler)
    
    # Step 4: Display results and plot predictions
    display_results_table(results)
    plot_predictions(all_predictions, output_features)

Related posts, You May like to read