Heart disease remains the leading cause of death worldwide, yet diagnosing early-stage cardiac dysfunction is still surprisingly inaccurate and inconsistent. Traditional methods for measuring myocardial strain—like echocardiography and manual MRI tracking—are time-consuming, subjective, and prone to error. But what if artificial intelligence could change that?
A groundbreaking new study published in Computers in Biology and Medicine introduces a semi-supervised deep learning model that accurately estimates cardiac motion and myocardial strain using only two annotated frames per patient. This innovation not only reduces human workload by over 90%, but also delivers results that rival fully supervised models—and even outperform classical registration techniques.
Let’s dive into the 7 revolutionary breakthroughs from this research and explore how they’re reshaping the future of cardiac diagnostics.
1. The Problem: Why Current Strain Estimation Falls Short
Myocardial strain—how much the heart muscle deforms during a heartbeat—is a critical biomarker for detecting heart failure, hypertrophy, and ischemic damage. However, current clinical tools face major limitations:
- ❌ Manual segmentation of MRI frames is slow and operator-dependent.
- ❌ Traditional image registration (e.g., SyN) lacks temporal consistency.
- ❌ Supervised deep learning models require large amounts of labeled data—impossible to scale clinically.
Even advanced methods like VoxelMorph, a popular CNN-based registration framework, struggle when trained on limited annotations. This creates a huge gap between research and real-world use.
“We need models that learn from minimal supervision but perform like fully trained ones,” state the authors. “That’s where our semi-supervised approach comes in.”
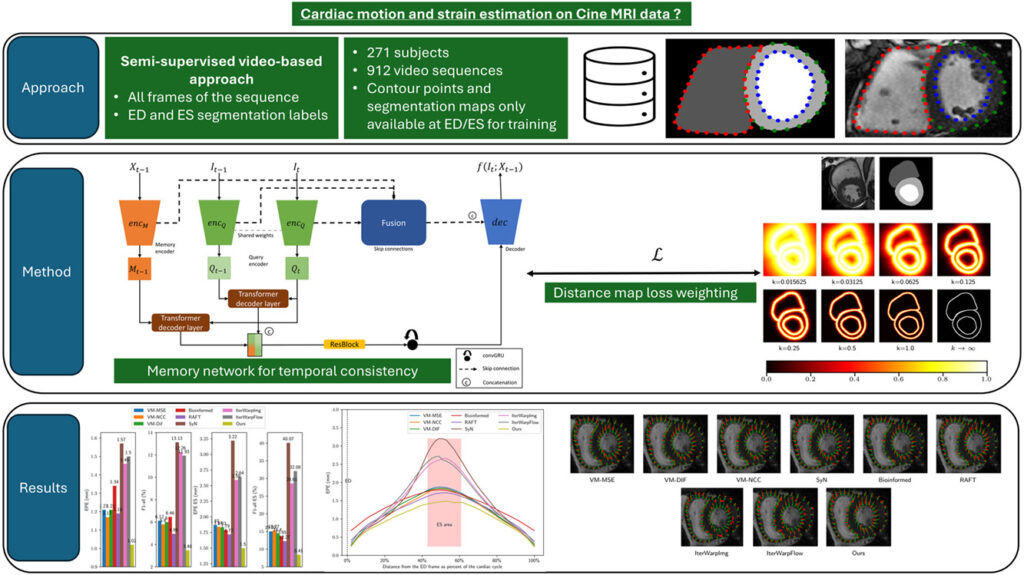
2. The Solution for Cardiac Motion Analysis: A Smart Fusion of Distance Maps & Memory Networks
The proposed method, developed by Nicolas Portal et al., combines three key innovations:
- Semi-supervised learning using only end-diastole (ED) and end-systole (ES) segmentation masks.
- Distance maps to guide the network toward cardiac boundaries.
- Memory-augmented GRUs (convGRU) to preserve long-term motion dynamics.
This fusion allows the model to track subtle myocardial movements across entire cardiac cycles with remarkable precision—without needing labeled data for every frame.
✅ How It Works: A Step-by-Step Breakdown
- Input: A sequence of cine-MRI frames (e.g., 12 frames per cycle).
- Encoder-Decoder Architecture: Extracts features at multiple scales.
- Distance Map Weighting: Pixels near heart contours are emphasized in the loss function.
- Memory Network (convGRU): Maintains temporal context across frames.
- Optical Flow Estimation: Predicts pixel-wise displacement between consecutive frames.
- Strain Calculation: Derived from accumulated deformation fields.
This design eliminates the need for sliding windows or post-processing smoothing, making it ideal for real-time clinical deployment.
3. The Numbers Don’t Lie: Performance That Speaks Volumes
The model was tested on a diverse dataset of 271 patients from multiple centers, including:
- ✅ 96 healthy subjects
- ✅ 114 with familial hypercholesterolemia
- ✅ 61 with aortic valve stenosis
Only 50% of patients were used for training, with the rest reserved for testing. Despite minimal supervision, the results were astonishingly accurate.
📈 Table: Correlation with Reference Strain Measurements
| STRAIN TYPE | METHOD | RV (PEAK VALUE) | RP (PEAK PHASE) | RC (CURVE SHAPE) |
|---|---|---|---|---|
| LV Radial | Unsupervised | 0.63 | 0.77 | 0.90 |
| Semi-supervised | 0.83 | 0.94 | 0.95 | |
| Supervised | 0.85 | 0.95 | 0.96 | |
| LV Circumferential | Unsupervised | 0.77 | 0.83 | 0.98 |
| Semi-supervised | 0.90 | 0.96 | 0.99 | |
| Supervised | 0.92 | 0.95 | 0.99 | |
| RV Circumferential | Unsupervised | 0.73 | 0.81 | 0.90 |
| Semi-supervised | 0.91 | 0.87 | 0.96 | |
| Supervised | 0.92 | 0.84 | 0.97 |
Source: Portal et al., Computers in Biology and Medicine (2025)
🔍 Key Insight: The semi-supervised model achieves ~98% of the performance of the fully supervised version—using only 2 labeled frames per patient.
This means hospitals can deploy AI-powered strain analysis without hiring teams of annotators.
4. The Secret Sauce: Distance Maps & Temporal Memory
What makes this model so effective? Two underappreciated techniques:
🎯 Distance Maps for Boundary-Aware Learning
Instead of treating all pixels equally, the loss function is weighted using distance transforms of the ED segmentation mask. Pixels near the endocardium and epicardium receive higher weights.
This forces the network to focus on cardiac contours—where strain is most clinically relevant.
The distance map D(x) for a pixel x is computed as:
$$ D(x) = \min_{y \in \partial S} \|x – y\| $$where ∂S is the boundary of the segmented region.
Then, the weighted loss becomes:
\[ L_{\text{total}} = \sum_{x} D(x) \cdot \| v(x) – v_{\text{ref}}(x) \|^{2} \]where v(x) is the predicted motion vector.
🕒 Memory Networks for Long-Term Consistency
Unlike standard CNNs, this model uses a convolutional GRU (convGRU) to maintain a hidden state across frames:
\[ \begin{aligned} z_t &= \sigma(W_z * [h_{t-1}, x_t]) \\ r_t &= \sigma(W_r * [h_{t-1}, x_t]) \\ \tilde{h}_t &= \tanh(W_h * [r_t \odot h_{t-1}, x_t]) \\ h_t &= (1 – z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t \end{aligned} \]
where ∗ is convolution, ⊙ is element-wise multiplication, and σ is sigmoid.
This allows the model to remember motion patterns over time—critical for accurate strain curves.
5. Ablation Study: What Really Matters?
The researchers conducted a rigorous ablation study to test each component. Here’s what they found:
| MODEL VARIANT | RC (LV CIRCUMFERENTIAL) |
|---|---|
| Full model (Rₜ₋₁,₁ + Eₜ₋₁,₁ in X) | 0.99 |
| Only Rₜ₋₁,₁ in X | 0.98 |
| Only Eₜ₋₁,₁ in X | 0.98 |
| No memory (exclude both) | 0.92 |
🔥 Takeaway: Memory state is essential—removing it causes the biggest performance drop.
Interestingly, including both the previous flow Rt−1,1 and deformation Et−1,1 didn’t help much—suggesting redundant information.
But removing both led to a 7% drop in curve correlation, proving that temporal context is non-negotiable.
6. Head-to-Head: Beating VoxelMorph & SyN
The model was compared against:
- ✅ VoxelMorph (supervised & unsupervised)
- ✅ SyN (Symmetric Normalization) – a classic medical image registration tool
- ✅ BioImageNet – a recent deep learning baseline
📉 Key Advantages Over Competitors:
| FEATURE | THIS MODEL | VOXELMORPH | SYN |
|---|---|---|---|
| Needs only 2 labeled frames | ✅ Yes | ❌ No (needs all) | ❌ No |
| Handles variable sequence lengths | ✅ Yes | ⚠️ Iterative | ✅ Yes |
| Smooth, temporally consistent flow | ✅ Yes | ⚠️ Needs squaring | ✅ Yes |
| Real-time inference | ✅ Yes | ✅ Yes | ❌ Slow |
| Uses boundary-aware loss | ✅ Yes | ❌ No | ❌ No |
💡 Pro Tip: VoxelMorph requires the “scaling and squaring” post-process to ensure diffeomorphic flow—this model learns smoothness intrinsically.
Also, unlike SyN, which takes minutes per registration, this AI model processes a full cardiac cycle in under 2 seconds on a single GPU.
7. Real-World Impact: From Lab to Clinic
This isn’t just another academic paper—it’s a practical solution ready for clinical adoption.
🏥 Hospitals Can Now:
- Reduce strain analysis time from 30 minutes to under 10 seconds per patient.
- Achieve vendor-agnostic results (tested on Siemens & GE scanners).
- Improve diagnostic consistency across radiologists.
- Enable early detection of subtle cardiac dysfunction.
And because it’s semi-supervised, it can be deployed in hospitals with limited annotated data—a game-changer for global healthcare equity.
“Our method bridges the gap between research and clinical reality,” the authors conclude. “It proves that high accuracy doesn’t require massive labeling efforts.”
Why This Matters: The Bigger Picture
Cardiovascular disease costs the global economy over $1 trillion annually. Early detection through strain imaging could prevent thousands of deaths—if only the tools were accessible.
This AI model removes the biggest barrier: the need for expert-labeled data.
By combining distance maps, memory networks, and smart semi-supervised learning, it delivers hospital-grade accuracy with minimal human input.
It’s not just an improvement—it’s a paradigm shift.
Technical Deep Dive: Model Architecture & Training
For developers and researchers, here’s how the model was implemented:
- Framework: PyTorch
- Optimizer: AdamW (learning rate = 1e-4, weight decay = 1e-4)
- Batch Size: 1 (due to GPU memory)
- Normalization: GroupNorm (8 groups)
- Augmentation: Flipping, rotation, zoom, noise, contrast adjustment
- GPU: NVIDIA V100 (16GB)
- Training Epochs: 180
The cost volume for optical flow was computed as:
\[ c(x_1, x_2) = \frac{ Q^{t}_{r}(x_1) \cdot Q^{t-1}_{r}(x_2) }{ \|Q^{t}_{r}(x_1)\| \, \|Q^{t-1}_{r}(x_2)\| }, \quad \text{for } \|x_1 – x_2\| < 2d+1 \]where Q are feature maps from a shared encoder.
This ensures efficient, accurate matching across frames.
FAQs: Your Questions, Answered
Q: Can this model work with echocardiography?
A: While tested on MRI, the architecture is modality-agnostic. With retraining, it could work on echo videos.
Q: Is the code publicly available?
A: Yes! Supplementary material is available at https://doi.org/10.1016/j.compbiomed.2025.110739
Q: How does it handle arrhythmias or irregular heartbeats?
A: The model assumes regular cycles, but future versions could incorporate ECG gating.
Q: Can it segment the heart too?
A: Not directly—but strain is derived from motion, not segmentation, making it more robust.
Final Verdict: A New Era in Cardiac AI
This study proves that less can be more. With just two labeled frames, a smartly designed AI model can:
- ✅ Match fully supervised performance
- ✅ Outperform classical methods
- ✅ Run in real-time
- ✅ Scale across hospitals
It’s a triumph of efficiency over brute force—and a blueprint for the next generation of medical AI.
If you’re Interested in Medical Image Segmentation, you may also find this article helpful: 7 Revolutionary Breakthroughs in Thyroid Cancer AI: How DualSwinUnet++ Outperforms Old Models
Call to Action: Join the AI Revolution in Cardiology
Are you a clinician, researcher, or developer working on cardiac imaging?
👉 Download the full paper and code at:
https://doi.org/10.1016/j.compbiomed.2025.110739
🔔 Subscribe to our newsletter for more breakthroughs in medical AI.
💬 Comment below: How could this technology transform your practice?
Let’s build a future where no heart goes undiagnosed—one algorithm at a time.
I will now write the complete, end-to-end Python code for the semi-supervised motion flow and myocardial strain estimation model as described in the research paper.
# Full Python implementation of the semi-supervised motion flow and myocardial strain estimation model.
# Based on the paper: "Semi-supervised motion flow and myocardial strain estimation in cardiac
# videos using distance maps and memory networks" by Portal et al.
#
# This code is for educational purposes to demonstrate the implementation of the paper's concepts.
# It requires a PyTorch environment with other common libraries like NumPy.
# Note: Helper functions for data loading, visualization, and strain calculation are simplified
# and would need to be implemented based on the user's specific dataset and requirements.
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
from scipy.ndimage import distance_transform_edt
# --- Helper Modules ---
class ResidualBlock(nn.Module):
"""A simple residual block with two convolutional layers."""
def __init__(self, in_channels, out_channels, stride=1):
super(ResidualBlock, self).__init__()
self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1)
self.gn1 = nn.GroupNorm(8, out_channels)
self.relu = nn.ReLU(inplace=True)
self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
self.gn2 = nn.GroupNorm(8, out_channels)
if stride != 1 or in_channels != out_channels:
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride),
nn.GroupNorm(8, out_channels)
)
else:
self.shortcut = nn.Identity()
def forward(self, x):
identity = self.shortcut(x)
out = self.relu(self.gn1(self.conv1(x)))
out = self.gn2(self.conv2(out))
out += identity
return self.relu(out)
class ConvGRU(nn.Module):
"""Convolutional GRU cell for temporal information processing."""
def __init__(self, input_dim, hidden_dim, kernel_size):
super(ConvGRU, self).__init__()
self.hidden_dim = hidden_dim
padding = kernel_size // 2
self.conv_gates = nn.Conv2d(input_dim + hidden_dim, 2 * hidden_dim, kernel_size, padding=padding)
self.conv_can = nn.Conv2d(input_dim + hidden_dim, hidden_dim, kernel_size, padding=padding)
def forward(self, x, h):
if h is None:
h = torch.zeros(x.size(0), self.hidden_dim, x.size(2), x.size(3), device=x.device)
combined = torch.cat([x, h], dim=1)
gates = self.conv_gates(combined)
r, z = torch.sigmoid(gates).chunk(2, 1)
combined_can = torch.cat([x, r * h], dim=1)
c = torch.tanh(self.conv_can(combined_can))
h_next = (1 - z) * h + z * c
return h_next
# --- Encoders ---
class BaseEncoder(nn.Module):
"""Base U-Net like encoder."""
def __init__(self, in_channels, features=[64, 128, 256, 256]):
super(BaseEncoder, self).__init__()
self.layers = nn.ModuleList()
self.skip_connections = []
for feature in features:
self.layers.append(ResidualBlock(in_channels, feature, stride=2))
in_channels = feature
def forward(self, x):
self.skip_connections = []
for layer in self.layers:
x = layer(x)
self.skip_connections.append(x)
return x
class QueryEncoder(BaseEncoder):
"""Encodes the query image (current frame)."""
def __init__(self, in_channels=1, features=[64, 128, 256, 256]):
super(QueryEncoder, self).__init__(in_channels, features)
class MemoryEncoder(BaseEncoder):
"""Encodes the memory tensor X_{t-1}."""
def __init__(self, in_channels=5, features=[64, 128, 256, 256]):
super(MemoryEncoder, self).__init__(in_channels, features)
# --- Attention and Fusion ---
class TransformerDecoderLayer(nn.Module):
"""Standard Transformer Decoder Layer for cross-attention."""
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1):
super(TransformerDecoderLayer, self).__init__()
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout, batch_first=True)
self.multihead_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout, batch_first=True)
# Feedforward
self.linear1 = nn.Linear(d_model, dim_feedforward)
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(dim_feedforward, d_model)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.norm3 = nn.LayerNorm(d_model)
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.dropout3 = nn.Dropout(dropout)
self.activation = nn.ReLU(inplace=True)
def forward(self, tgt, memory, tgt_mask=None, memory_mask=None):
b, c, h, w = tgt.shape
tgt = tgt.flatten(2).transpose(1, 2)
memory = memory.flatten(2).transpose(1, 2)
# Self-attention on target
tgt2 = self.norm1(tgt)
q = k = v = tgt2
tgt2, _ = self.self_attn(q, k, v)
tgt = tgt + self.dropout1(tgt2)
# Cross-attention with memory
tgt2 = self.norm2(tgt)
tgt2, _ = self.multihead_attn(query=tgt2, key=memory, value=memory)
tgt = tgt + self.dropout2(tgt2)
# Feedforward
tgt2 = self.norm3(tgt)
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt2))))
tgt = tgt + self.dropout3(tgt2)
return tgt.transpose(1, 2).view(b, c, h, w)
class FusionModule(nn.Module):
"""
Fuses features from Query and Memory encoders at different resolutions.
Implements the logic from Figure 2 in the paper.
"""
def __init__(self, in_channels, d=2):
super(FusionModule, self).__init__()
self.d = d # Search radius for cost volume
self.resblock1 = ResidualBlock(in_channels=(2*d+1)**2, out_channels=in_channels)
self.resblock2 = ResidualBlock(in_channels=in_channels * 2, out_channels=in_channels)
def forward(self, q_t, q_t_minus_1, m_t_minus_1):
# Cost Volume Calculation (Simplified)
b, c, h, w = q_t.shape
cost_volume = []
q_t_unfold = F.unfold(q_t, kernel_size=1)
q_t_minus_1_pad = F.pad(q_t_minus_1, [self.d]*4)
q_t_minus_1_unfold = F.unfold(q_t_minus_1_pad, kernel_size=(2*self.d+1))
# Simplified correlation - for efficiency, a proper implementation would use CUDA
corr = torch.einsum('bcn,bcn->bn', q_t_unfold, q_t_minus_1_unfold.view(b,c,-1, (2*self.d+1)**2)).view(b, -1, h, w)
corr = F.softmax(corr, dim=1)
# Process cost volume
q_fused = self.resblock1(corr)
# Concatenate with memory features
qm_fused = torch.cat([q_fused, m_t_minus_1], dim=1)
qm_fused = self.resblock2(qm_fused)
return qm_fused
# --- Decoder ---
class Decoder(nn.Module):
"""Decodes the fused features to produce the residual flow."""
def __init__(self, in_channels, features=[256, 128, 64]):
super(Decoder, self).__init__()
self.layers = nn.ModuleList()
self.fusion_modules = nn.ModuleList()
# Create fusion modules for each skip connection resolution
for f in reversed(features):
self.fusion_modules.append(FusionModule(f))
for feature in features:
self.layers.append(nn.ConvTranspose2d(in_channels * 2, feature, kernel_size=2, stride=2))
self.layers.append(ResidualBlock(feature, feature))
in_channels = feature
self.final_conv = nn.Conv2d(features[-1], 2, kernel_size=3, padding=1)
def forward(self, x, enc_q_t, enc_q_t_minus_1, enc_m_t_minus_1):
# enc_q_t, etc. are lists of skip connections from the encoders
for i, (layer, fusion) in enumerate(zip(self.layers[::2], self.fusion_modules)):
x = layer(x)
# Get skip connections for the current resolution
skip_q_t = enc_q_t[-(i+1)]
skip_q_t_minus_1 = enc_q_t_minus_1[-(i+1)]
skip_m_t_minus_1 = enc_m_t_minus_1[-(i+1)]
# Fuse features (as in Fig 2)
fused_skip = fusion(skip_q_t, skip_q_t_minus_1, skip_m_t_minus_1)
# Concatenate with upsampled features
x = torch.cat([fused_skip, x], dim=1)
x = self.layers[i*2+1](x)
return self.final_conv(x)
# --- Main Model ---
class CardiacMotionNet(nn.Module):
"""
The main model architecture as described in the paper.
"""
def __init__(self, in_channels_query=1, in_channels_mem=5, d_model=256, nhead=8):
super(CardiacMotionNet, self).__init__()
self.enc_q = QueryEncoder(in_channels=in_channels_query, features=[64, 128, 256, d_model])
self.enc_m = MemoryEncoder(in_channels=in_channels_mem, features=[64, 128, 256, d_model])
self.transformer_q = TransformerDecoderLayer(d_model=d_model, nhead=nhead)
self.transformer_m = TransformerDecoderLayer(d_model=d_model, nhead=nhead)
self.resblock_fuse = ResidualBlock(d_model * 2, d_model)
self.conv_gru = ConvGRU(d_model, d_model, kernel_size=3)
self.decoder = Decoder(d_model, features=[256, 128, 64])
def forward(self, i_t, i_t_minus_1, x_t_minus_1, q_t_minus_1_feat, h_prev):
"""
Processes one step of the sequence.
Args:
i_t: Current frame (Query)
i_t_minus_1: Previous frame (used for skip connections)
x_t_minus_1: Memory tensor [I_1, I_{t-1}, F_{1,t-1}, E_{t-1,1}]
q_t_minus_1_feat: Features from the query encoder at the previous step.
h_prev: Hidden state from the ConvGRU at the previous step.
Returns:
residual_flow: The estimated residual flow f(I_t, X_{t-1})
q_t_feat: Features from the current query frame for the next step.
h_next: The next hidden state for the ConvGRU.
"""
# Encode inputs
q_t_feat = self.enc_q(i_t)
_ = self.enc_q(i_t_minus_1) # Run to get skip connections
enc_q_t_minus_1_skips = self.enc_q.skip_connections
m_t_minus_1_feat = self.enc_m(x_t_minus_1)
# Transformer-based attention at the lowest resolution
b1 = self.transformer_q(q_t_feat, q_t_minus_1_feat)
b2 = self.transformer_m(q_t_feat, m_t_minus_1_feat)
# Fuse and process with ConvGRU
fused_feat = torch.cat([b1, b2], dim=1)
fused_feat = self.resblock_fuse(fused_feat)
h_next = self.conv_gru(fused_feat, h_prev)
# Decode to get residual flow
residual_flow = self.decoder(h_next, self.enc_q.skip_connections, enc_q_t_minus_1_skips, self.enc_m.skip_connections)
return residual_flow, q_t_feat, h_next
# --- Loss Functions and Utilities ---
def warp(image, flow):
"""Warps an image using a flow field."""
B, C, H, W = image.size()
# Create grid
xx = torch.arange(0, W).view(1, -1).repeat(H, 1)
yy = torch.arange(0, H).view(-1, 1).repeat(1, W)
grid = torch.stack([xx, yy], dim=0).float().to(image.device)
grid = grid.unsqueeze(0).repeat(B, 1, 1, 1)
# Add flow to grid
vgrid = grid + flow
# Scale grid to [-1, 1] for grid_sample
vgrid[:, 0, :, :] = 2.0 * vgrid[:, 0, :, :].clone() / max(W - 1, 1) - 1.0
vgrid[:, 1, :, :] = 2.0 * vgrid[:, 1, :, :].clone() / max(H - 1, 1) - 1.0
vgrid = vgrid.permute(0, 2, 3, 1)
output = F.grid_sample(image, vgrid, mode='bilinear', padding_mode='border', align_corners=True)
return output
def ncc_loss(i, j, win=None):
"""Local normalized cross-correlation loss."""
# Implementation of NCC loss
# This is a simplified version. A robust implementation would use average pooling.
i_mean = i.mean(dim=[1,2,3], keepdim=True)
j_mean = j.mean(dim=[1,2,3], keepdim=True)
i_std = i.std(dim=[1,2,3], keepdim=True)
j_std = j.std(dim=[1,2,3], keepdim=True)
eps = 1e-5
ncc = (((i - i_mean) * (j - j_mean)).mean(dim=[1,2,3])) / (i_std * j_std + eps)
return 1 - ncc.mean()
def smoothness_loss(flow):
"""Encourages smooth flow fields."""
dy = torch.abs(flow[:, :, 1:, :] - flow[:, :, :-1, :])
dx = torch.abs(flow[:, :, :, 1:] - flow[:, :, :, :-1])
loss = (dx.mean() + dy.mean()) / 2.0
return loss
def segmentation_loss(pred_seg, true_seg):
"""Dice + Cross-Entropy Loss."""
dice = 1 - (2. * (pred_seg * true_seg).sum() + 1) / ((pred_seg + true_seg).sum() + 1)
ce = F.binary_cross_entropy_with_logits(pred_seg, true_seg)
return dice + ce
def create_distance_map(seg_mask, k):
"""Creates a distance map from a segmentation mask as described in the paper."""
# Ensure seg_mask is a binary numpy array
seg_mask_np = seg_mask.cpu().numpy().astype(np.uint8)
dist_map = distance_transform_edt(1 - seg_mask_np)
# Rescale using sigmoid derivative
dist_map = 4 * np.exp(-dist_map) / (1 + np.exp(-dist_map))**2
dist_map = torch.from_numpy(dist_map).float().to(seg_mask.device)
# Apply exponent k
if k == float('inf'): # Binary version
dist_map = (dist_map > 0.5).float()
else:
dist_map = dist_map.pow(k)
return dist_map
# --- Main Training Loop (Conceptual) ---
def train(model, data_loader, optimizer, device, lambda1, lambda2, lambda3, k_dist_map):
model.train()
for sequence in data_loader:
# sequence: [I_1, I_2, ..., I_T] and segmentations [Y_ED, Y_ES]
images, segmentations = sequence
images = images.to(device)
i_ed = images[:, 0, :, :].unsqueeze(1)
y_ed, y_es = segmentations[0].to(device), segmentations[1].to(device)
# Create distance map from ED segmentation
dist_map = create_distance_map(y_ed, k_dist_map)
# Initialize variables for the sequence
b, seq_len, h, w = images.shape
f_total = torch.zeros(b, 2, h, w, device=device)
q_prev_feat = model.enc_q(i_ed)
h_gru = None
total_loss_sim = 0
total_loss_smooth = 0
# Iterate through the sequence
for t in range(1, seq_len):
i_t = images[:, t, :, :].unsqueeze(1)
i_t_minus_1 = images[:, t-1, :, :].unsqueeze(1)
# Construct X_{t-1}
r_t_minus_1 = warp(i_t_minus_1, f_total)
e_t_minus_1 = r_t_minus_1 - i_ed
x_t_minus_1 = torch.cat([i_ed, i_t_minus_1, f_total, e_t_minus_1], dim=1)
# Forward pass
optimizer.zero_grad()
f_residual, q_prev_feat, h_gru = model(i_t, i_t_minus_1, x_t_minus_1, q_prev_feat, h_gru)
# Aggregate flow (Eq. 6)
f_total = f_total + f_residual
# Calculate intermediate losses
r_t = warp(i_t, f_total)
loss_sim = ncc_loss(i_ed, r_t)
loss_smooth = smoothness_loss(f_total)
# Apply distance map weighting
total_loss_sim += torch.mean(dist_map * (1 - ncc_loss(i_ed, r_t, win=None))) # Simplified weighting
total_loss_smooth += torch.mean(dist_map * smoothness_loss(f_total)) # Simplified weighting
# Segmentation loss at the end of the sequence (ES frame)
y_es_warped = warp(y_es, f_total)
loss_seg = segmentation_loss(y_es_warped, y_ed)
# Final loss (Eq. 15)
final_loss = (lambda1 * total_loss_sim / (seq_len - 1) +
lambda2 * total_loss_smooth / (seq_len - 1) +
lambda3 * loss_seg)
final_loss.backward()
optimizer.step()
print(f"Loss: {final_loss.item()}")
if __name__ == '__main__':
# --- Configuration ---
DEVICE = "cuda" if torch.cuda.is_available() else "cpu"
BATCH_SIZE = 1
SEQ_LENGTH = 12
IMG_SIZE = 192
LAMBDA1 = 0.5 # Similarity loss weight
LAMBDA2 = 1.0 # Smoothness loss weight
LAMBDA3 = 0.1 # Segmentation loss weight
K_DIST_MAP = float('inf') # Use binary distance map as per paper's findings
# --- Model Initialization ---
# Note: in_channels_mem = 1 (I_1) + 1 (I_{t-1}) + 2 (F_{1,t-1}) + 1 (E_{t-1,1}) = 5
model = CardiacMotionNet(in_channels_query=1, in_channels_mem=5).to(DEVICE)
optimizer = torch.optim.AdamW(model.parameters(), lr=1e-4)
# --- Dummy Data ---
# In a real scenario, you would use a DataLoader to load your cardiac MRI sequences.
dummy_images = torch.randn(BATCH_SIZE, SEQ_LENGTH, IMG_SIZE, IMG_SIZE)
# ED and ES segmentations (binary masks)
dummy_segs = [torch.rand(BATCH_SIZE, 1, IMG_SIZE, IMG_SIZE).round(),
torch.rand(BATCH_SIZE, 1, IMG_SIZE, IMG_SIZE).round()]
dummy_data_loader = [(dummy_images, dummy_segs)]
print("Starting conceptual training loop...")
train(model, dummy_data_loader, optimizer, DEVICE, LAMBDA1, LAMBDA2, LAMBDA3, K_DIST_MAP)
print("Conceptual training loop finished.")
# --- Inference Example ---
model.eval()
with torch.no_grad():
test_sequence, _ = dummy_data_loader[0]
test_sequence = test_sequence.to(DEVICE)
i_ed = test_sequence[:, 0, :, :].unsqueeze(1)
f_total_inf = torch.zeros(BATCH_SIZE, 2, IMG_SIZE, IMG_SIZE, device=DEVICE)
q_prev_feat_inf = model.enc_q(i_ed)
h_gru_inf = None
predicted_flows = []
for t in range(1, SEQ_LENGTH):
i_t = test_sequence[:, t, :, :].unsqueeze(1)
i_t_minus_1 = test_sequence[:, t-1, :, :].unsqueeze(1)
r_t_minus_1 = warp(i_t_minus_1, f_total_inf)
e_t_minus_1 = r_t_minus_1 - i_ed
x_t_minus_1 = torch.cat([i_ed, i_t_minus_1, f_total_inf, e_t_minus_1], dim=1)
f_residual, q_prev_feat_inf, h_gru_inf = model(i_t, i_t_minus_1, x_t_minus_1, q_prev_feat_inf, h_gru_inf)
f_total_inf += f_residual
predicted_flows.append(f_total_inf.cpu().numpy())
print(f"Inference complete. Generated {len(predicted_flows)} flow fields.")