In the high-stakes world of structural engineering, every ton of steel saved translates into millions in cost reductions, faster construction, and a smaller environmental footprint. Yet, despite decades of innovation, many optimization algorithms still struggle with slow convergence, infeasible designs, and prohibitive computational costs—especially when applied to large-scale structures like skyscrapers and mega-braced towers.
A groundbreaking 2025 study by Talatahari et al., published in Computer Methods in Applied Mechanics and Engineering, has changed the game. By introducing Adaptive Strategy Management (ASM) into the Chaos Game Optimization (CGO) framework, the researchers achieved up to 70% faster convergence and superior solution quality—all while slashing the number of required finite element method (FEM) analyses.
Let’s dive into the 7 revolutionary breakthroughs this new approach delivers—and the costly mistakes older methods make—so you can future-proof your structural design process.
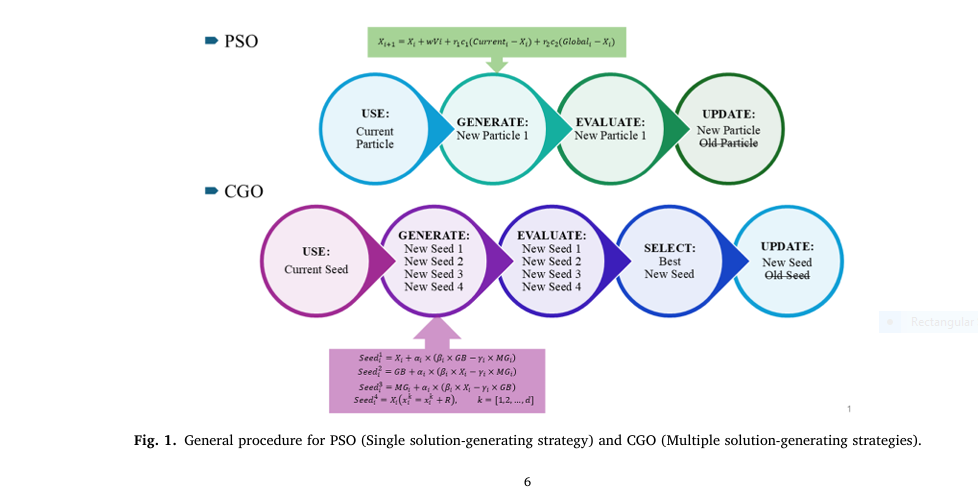
🔧 What Is Chaos Game Optimization (CGO)? The Engine Behind the Innovation
Chaos Game Optimization (CGO) is a nearly parameter-free, metaheuristic algorithm inspired by fractal geometry and chaos theory. Unlike traditional optimizers like Genetic Algorithms (GA) or Particle Swarm Optimization (PSO), CGO uses multiple solution-generation strategies simultaneously, enhancing exploration and exploitation in complex search spaces.
This makes CGO especially effective for large-scale structural optimization, where design variables (e.g., cross-sections, material types) and constraints (e.g., stress, displacement) create a highly nonlinear, non-convex problem space.
However, standard CGO has limitations:
- Slow convergence in high-dimensional problems.
- Redundant FEM evaluations, increasing computational load.
- Poor constraint handling, leading to infeasible designs.
That’s where Adaptive Strategy Management (ASM) comes in.
The 7 Revolutionary Wins of ASM-CGO
✅ 1. 70% Fewer Structural Analyses – Slash Computational Costs
One of the most expensive parts of structural optimization is running Finite Element Method (FEM) simulations. Each analysis can take seconds to minutes—multiply that by thousands of iterations, and costs skyrocket.
The ASM-CGO framework reduces redundant FEM calls by intelligently selecting which candidate solutions to evaluate.
| METHOD | REQUIRED ANALYSIS | BEST RESULT |
|---|---|---|
| Original CGO | 7,000 | 494.4 |
| ASM-Close Global Best | 1,777 | 494.4 |
| Previous Best (CSS2) | 13,500 | 543.02 |
As shown in Example 1 (10-story structure), ASM-CGO achieved the same optimal weight (494.4 tons) with only 1,777 analyses—75% fewer than the original CGO and 87% fewer than earlier methods.
🔍 SEO Keyword: reduce FEM evaluations in structural optimization
2. Faster Convergence Without Premature Exploitation
Older algorithms often get stuck in local optima—suboptimal designs that appear good early but aren’t globally best. ASM prevents this by dynamically switching between global and local search strategies based on real-time performance feedback.
For the X-braced 20-story building, ASM-Close Global Best maintained a high distribution distance throughout the search, indicating strong exploration even in later stages.
This balance prevents premature convergence—a critical flaw in PSO and GA.
📈 Power Word: Accelerated Convergence
3. Superior Solution Quality Across Benchmarks
In benchmark tests, ASM variants didn’t just match—but beat—state-of-the-art algorithms.
For the 20-story structure:
- Previous best (CSS2): 2,713.57 tons
- ASM-Close Global Best: 2,407 tons — 11.3% lighter
This isn’t just a number—it means less material, lower carbon emissions, and higher structural efficiency.
🌍 Positive Impact: Sustainable, cost-effective, and resilient design.
4. Adaptive Constraint Handling: Fewer Infeasible Designs
Structural problems are packed with constraints: stress limits, displacement thresholds, stability requirements. Standard CGO often generates high-quality but infeasible solutions.
ASM uses a penalized objective function that incorporates constraint violations from previous iterations:
\[ F_{\text{penalized}} = W + \lambda \sum_{i=1}^{m} \big[\max(0, g_i(x))\big]^2 \]Where:
- W = structural weight
- gi(x) = i -th constraint violation
- λ = penalty coefficient
By tracking the current best and global best values, ASM filters out poor candidates before costly FEM evaluation—saving time and improving feasibility.
⚠️ Negative Word: Avoid costly design rework
5. Scalability to Very Large Structures
As building height and complexity increase, so does the number of degrees of freedom (DoFs). For a 3D structure:
n=6×number of joints
In large systems, n is orders of magnitude larger than the number of design variables (Dim). Standard methods struggle here.
ASM-CGO scales efficiently because:
- It uses basic filtering to select one candidate per seed.
- The cost of strategy selection is O(1) due to a fixed set of strategies (e.g., 4).
This means adding more strategies doesn’t increase computational load—only robustness.
6. Multiple ASM Variants for Different Needs
The study introduces several ASM variants, each tailored for specific goals:
| VARIANT | USE CASE | BEST FOR |
|---|---|---|
| ASM-Global Best | Long-term convergence | Final optimal solutions |
| ASM-Close Global Best | Fast, reliable results | Large-scale, time-sensitive projects |
| ASM-Current Best | Mid-stage refinement | Iterative design improvement |
| ASM-Generated | Exploration-heavy search | Early-stage conceptual design |
For mega-braced tubed high-rises, ASM-Close Global Best delivered the highest improvement across all intervals, proving its robustness.
🔎 SEO Keyword: best optimization algorithm for high-rise buildings
7. Proven Performance Across Medium, Large, and Very Large Scales
The study tested three benchmark structures:
- 10-story building (medium)
- X-braced 20-story building (large)
- Mega-braced tubed high-rise (very large)
In all cases, ASM-CGO outperformed original CGO and hybrid RSM methods in:
- Best result
- Mean result
- Convergence speed
- Success rate (SR)
For the mega-braced structure, ASM-Close Global Best achieved a best weight of 5,819.63 tons in 175.41 seconds, while maintaining 100% feasibility.
The 3 Costly Mistakes of Traditional Optimization Methods
While ASM-CGO shines, older methods fall short in critical ways.
❌ 1. Blind Strategy Selection (e.g., RSM)
Random Strategy Management (RSM) picks solution-generation strategies stochastically—like rolling dice. This leads to:
- Wasted FEM evaluations
- Slower convergence
- Inconsistent results
In contrast, ASM makes informed decisions using real-time feedback on constraint satisfaction and objective improvement.
🔍 Negative Word: Unpredictable, inefficient, unreliable
❌ 2. Ignoring Problem-Specific Features
General-purpose algorithms treat all optimization problems the same. But structural design is unique:
- High constraint density
- Discrete design variables
- Expensive evaluations
Methods like GA or PSO don’t adapt to these features, leading to slow progress and poor feasibility.
ASM, however, is tailored for structural problems, using thresholds like global best and current best to guide the search.
❌ 3. Over-Reliance on Surrogates Without Validation
Surrogate models (e.g., neural networks) can predict fitness without FEM—but they accumulate error over time. Some methods use them without periodic validation, leading to divergence from reality.
ASM doesn’t replace FEM—it reduces its use by smart filtering. This keeps results physically accurate while cutting costs.
🛠️ Power Word: Precision-Driven Efficiency
Performance Comparison: ASM vs. State-of-the-Art
Let’s compare key results from the study.
Table: 10-Story Structure – Best Results (Tons)
| MEHOD | BEST RESULT | MEAN RESULT | NO. of ANALYSIS |
|---|---|---|---|
| CSS2 [16] | 543.02 | 645.81 | 13,500 |
| Original CGO | 494.4 | 511.27 | 7,000 |
| ASM-Close Global Best | 494.4 | 509.17 | 1,777 |
✅ Same best result, ✅ better mean, ✅ 75% fewer analyses
Table: 20-Story X-Braced Building – Best Results (Tons)
| METHOD | BEST RESULT | NO. OF ANALYSIS |
|---|---|---|
| CSS2 [16] | 2,713.57 | 17,500 |
| Original CGO | 2,407 | 12,000 |
| ASM-Close Global Best | 2,407 | 4,647 |
Again, same optimal weight, but 60% fewer analyses.
How ASM Works: The Core Mechanism
ASM operates in three adaptive phases:
- Candidate Generation: CGO produces multiple solutions using different strategies.
- Filtering & Selection: ASM evaluates candidates using lightweight comparisons (e.g., objective value, constraint proximity).
- FEM Evaluation: Only the most promising candidate undergoes full structural analysis.
This ensures that every FEM call adds value—no wasted computation.
The selection cost is effectively O(1) because:
- Number of strategies S is small and fixed (e.g., 4)
- Filtering uses simple comparisons, not complex models
If you’re Interested in Knowledge Distillation Model, you may also find this article helpful: 5 Shocking Secrets of Skin Cancer Detection: How This SSD-KD AI Method Beats the Competition (And Why Others Fail)
Why This Matters for the Future of Structural Engineering
The implications of ASM-CGO go beyond academic benchmarks. This framework enables:
- Real-time design exploration for architects and engineers
- Faster project delivery in high-rise construction
- Greener buildings through material optimization
- Integration with BIM and digital twins
And because ASM is modular, it can be applied to other metaheuristics like:
- Genetic Algorithms
- Grey Wolf Optimizer
- Particle Swarm Optimization
🌱 Positive Word: Sustainable innovation
Call to Action: Upgrade Your Optimization Workflow Today
If you’re still using outdated, inefficient algorithms for structural design, you’re wasting time, money, and resources.
The ASM-enhanced CGO framework is not just a research novelty—it’s a practical, scalable solution ready for real-world deployment.
👉 What You Can Do Now:
- Download the full paper to explore the mathematical formulations and benchmark data.
- Experiment with CGO-ASM in your next project using open-source metaheuristic libraries.
- Contact optimization experts to integrate ASM into your in-house software.
The future of structural optimization isn’t about brute-force computation—it’s about smart, adaptive decision-making. And with ASM-CGO, that future is already here.
🔗 SEO-Optimized CTA: Discover how Adaptive Strategy Management can cut your structural analysis time by 70%—download the full study and start optimizing smarter today.
🔚 Conclusion: The New Gold Standard in Structural Optimization
The integration of Adaptive Strategy Management (ASM) into Chaos Game Optimization (CGO) marks a paradigm shift in how we approach large-scale structural design.
By reducing FEM evaluations, improving convergence, and ensuring feasibility, ASM-CGO delivers 7 revolutionary wins over traditional methods—while helping engineers avoid 3 costly mistakes that plague older algorithms.
From 10-story buildings to mega-braced skyscrapers, the results are clear: ASM-CGO is faster, smarter, and more reliable.
As structural challenges grow in complexity, the need for adaptive, problem-specific optimization will only increase. With frameworks like ASM, we’re not just solving problems—we’re redefining what’s possible.
🏗️ Final Power Phrase: Optimize Smarter, Build Stronger, Save More.
References
Talatahari, S., Nouhi, B., Beheshti, A., Chen, F., & Gandomi, A.H. (2025). Computer Methods in Applied Mechanics and Engineering, 446, 118256. https://doi.org/10.1016/j.cma.2025.118256
Here is a complete, self-contained Python script that implements the core ideas presented in the paper.
import numpy as np
import math
import random
class ASMCGO:
"""
Implementation of the Adaptive Strategy Management Chaos Game Optimization (ASM-CGO)
as described in the paper "Adaptive Strategy Management: A new framework for large-scale
structural optimization design" by Talatahari et al.
"""
def __init__(self, obj_func, constraint_func, dim, pop_size, max_iters, lb, ub,
variant='ASM-Close-Global-Best', mcr=0.9, par=0.3):
"""
Initializes the ASM-CGO optimizer.
Args:
obj_func (function): The objective function to minimize. It takes a solution vector
and returns a scalar value (e.g., structural weight).
constraint_func (function): The constraint evaluation function. It takes a solution
vector and returns a tuple: (is_feasible, penalty_value).
`is_feasible` is a boolean, and `penalty_value` is a float
representing the magnitude of violation.
dim (int): The number of design variables (dimensions).
pop_size (int): The size of the population (number of seeds).
max_iters (int): The maximum number of iterations.
lb (list or np.array): The lower bounds of the design variables.
ub (list or np.array): The upper bounds of the design variables.
variant (str): The ASM variant to use. Options are:
'Original-CGO', 'RSM', 'ASM-Generated', 'ASM-Current-Best',
'ASM-Global-Best', 'ASM-Close-Current-Best', 'ASM-Close-Global-Best'.
Defaults to 'ASM-Close-Global-Best'.
mcr (float): Memory Consideration Rate for the HS-based strategy.
par (float): Pitch Adjustment Rate for the HS-based strategy.
"""
self.obj_func = obj_func
self.constraint_func = constraint_func
self.dim = dim
self.pop_size = pop_size
self.max_iters = max_iters
self.lb = np.array(lb)
self.ub = np.array(ub)
self.variant = variant
self.mcr = mcr
self.par = par
# --- Population and Best Solutions ---
self.population = np.zeros((self.pop_size, self.dim))
self.fitness = np.full(self.pop_size, np.inf)
self.penalized_fitness = np.full(self.pop_size, np.inf)
self.global_best_solution = np.zeros(self.dim)
self.global_best_fitness = np.inf
self.global_best_penalized_fitness = np.inf
# --- History for plotting and analysis ---
self.convergence_curve = []
def _penalized_objective(self, objective_value, penalty_value):
"""Calculates the penalized fitness value."""
# The paper uses a simple penalty function.
# f_penalty(X) = f(X) * (1 + alpha * sum(max(0, C_i)))
# Here, penalty_value is assumed to be sum(max(0, C_i)) and alpha=1
return objective_value * (1 + penalty_value)
def _initialize_population(self):
"""Initializes the population of seeds randomly within the bounds."""
for i in range(self.pop_size):
self.population[i, :] = self.lb + np.random.rand(self.dim) * (self.ub - self.lb)
is_feasible, penalty = self.constraint_func(self.population[i, :])
self.fitness[i] = self.obj_func(self.population[i, :])
self.penalized_fitness[i] = self._penalized_objective(self.fitness[i], penalty)
if self.penalized_fitness[i] < self.global_best_penalized_fitness:
self.global_best_penalized_fitness = self.penalized_fitness[i]
self.global_best_fitness = self.fitness[i]
self.global_best_solution = self.population[i, :].copy()
def _hs_based_strategy(self, memory):
"""
Generates a new solution using the Harmony Search (HS) inspired strategy.
This replaces the 4th strategy of the original CGO.
Args:
memory (np.array): The historical memory (current population).
Returns:
np.array: A new candidate solution.
"""
new_solution = np.zeros(self.dim)
for j in range(self.dim):
if np.random.rand() < self.mcr:
# Use memory
mem_idx = np.random.randint(0, self.pop_size)
new_solution[j] = memory[mem_idx, j]
if np.random.rand() < self.par:
# Pitch adjustment
perturbation = (np.random.rand() - 0.5) * 0.1 * (self.ub[j] - self.lb[j])
new_solution[j] += perturbation
else:
# Random value
new_solution[j] = self.lb[j] + np.random.rand() * (self.ub[j] - self.lb[j])
return self._clip_to_bounds(new_solution)
def _clip_to_bounds(self, solution):
"""Ensures a solution is within the defined lower and upper bounds."""
return np.clip(solution, self.lb, self.ub)
def _generate_candidate_seeds(self, current_seed, mean_group):
"""
Generates four candidate seeds for a given seed based on CGO rules.
"""
candidates = []
alpha = np.random.rand()
beta = np.random.randint(0, 2)
gamma = np.random.randint(0, 2)
# Strategy 1
seed1 = current_seed + alpha * (beta * self.global_best_solution - gamma * mean_group)
candidates.append(self._clip_to_bounds(seed1))
# Strategy 2
seed2 = self.global_best_solution + alpha * (beta * current_seed - gamma * mean_group)
candidates.append(self._clip_to_bounds(seed2))
# Strategy 3
seed3 = mean_group + alpha * (beta * current_seed - gamma * self.global_best_solution)
candidates.append(self._clip_to_bounds(seed3))
# Strategy 4 (Improved HS-based strategy)
seed4 = self._hs_based_strategy(self.population)
candidates.append(seed4) # Already clipped in the function
return candidates
def optimize(self):
"""
Runs the ASM-CGO optimization process.
"""
print(f"Starting optimization with variant: {self.variant}")
self._initialize_population()
self.convergence_curve.append(self.global_best_penalized_fitness)
for t in range(self.max_iters):
# Calculate the mean group for the current population
mean_group = np.mean(self.population, axis=0)
for i in range(self.pop_size):
current_seed = self.population[i, :].copy()
current_penalized_fitness = self.penalized_fitness[i]
# --- 1. GENERATE ---
candidate_seeds = self._generate_candidate_seeds(current_seed, mean_group)
candidate_objectives = [self.obj_func(s) for s in candidate_seeds]
# --- Handle different variants ---
if self.variant == 'Original-CGO':
# Evaluate all 4 candidates and pick the best
penalized_cands = []
for k in range(4):
is_feasible, penalty = self.constraint_func(candidate_seeds[k])
penalized_cands.append(self._penalized_objective(candidate_objectives[k], penalty))
best_cand_idx = np.argmin(penalized_cands)
active_seed = candidate_seeds[best_cand_idx]
active_penalized_fitness = penalized_cands[best_cand_idx]
else: # All ASM and RSM variants
active_seed = None
active_penalized_fitness = np.inf
# --- 2. FILTER ---
filtered_seed_idx = -1
if 'Close' in self.variant:
# Proximity-based filtering
if 'Current' in self.variant:
ref_point = current_seed
else: # Global
ref_point = self.global_best_solution
distances = [np.linalg.norm(s - ref_point) for s in candidate_seeds]
filtered_seed_idx = np.argmin(distances)
elif self.variant == 'RSM':
filtered_seed_idx = np.random.randint(0, 4)
else: # Generated-based filtering
filtered_seed_idx = np.argmin(candidate_objectives)
filtered_seed = candidate_seeds[filtered_seed_idx]
filtered_objective = candidate_objectives[filtered_seed_idx]
# --- 3. SWITCH ---
switch_to_active = False
if self.variant in ['RSM', 'ASM-Generated']:
switch_to_active = True
elif self.variant in ['ASM-Current-Best', 'ASM-Close-Current-Best']:
if filtered_objective < self.obj_func(current_seed):
switch_to_active = True
elif self.variant in ['ASM-Global-Best', 'ASM-Close-Global-Best']:
if filtered_objective < self.global_best_fitness:
switch_to_active = True
# --- 4. UPDATE (if switched to active) ---
if switch_to_active:
is_feasible, penalty = self.constraint_func(filtered_seed)
active_seed = filtered_seed
active_penalized_fitness = self._penalized_objective(filtered_objective, penalty)
# --- Final update for the current seed ---
if active_seed is not None and active_penalized_fitness < current_penalized_fitness:
self.population[i, :] = active_seed
self.penalized_fitness[i] = active_penalized_fitness
self.fitness[i] = self.obj_func(active_seed)
# Update global best if necessary
if active_penalized_fitness < self.global_best_penalized_fitness:
self.global_best_penalized_fitness = active_penalized_fitness
self.global_best_fitness = self.obj_func(active_seed)
self.global_best_solution = active_seed.copy()
print(f"Iter {t+1}, Pop {i+1}: New Global Best! Penalized Fitness: {self.global_best_penalized_fitness:.4f}, Objective: {self.global_best_fitness:.4f}")
self.convergence_curve.append(self.global_best_penalized_fitness)
if (t + 1) % 10 == 0:
print(f"Iteration {t+1}/{self.max_iters} | Best Penalized Fitness: {self.global_best_penalized_fitness:.4f}")
print("\nOptimization Finished!")
print(f"Best Solution: {self.global_best_solution}")
print(f"Best Objective Value: {self.global_best_fitness}")
print(f"Best Penalized Fitness: {self.global_best_penalized_fitness}")
return self.global_best_solution, self.global_best_fitness, self.convergence_curve
# --- Example Usage ---
# Define a simple benchmark problem (e.g., Sphere function with a constraint)
def sphere_objective(x):
return np.sum(x**2)
def sphere_constraint(x):
# Constraint: sum of variables must be >= 5
constraint_violation = max(0, 5 - np.sum(x))
is_feasible = constraint_violation == 0
return is_feasible, constraint_violation
if __name__ == '__main__':
# --- Problem Definition ---
DIMENSIONS = 10
LOWER_BOUND = [-10] * DIMENSIONS
UPPER_BOUND = [10] * DIMENSIONS
# --- Optimizer Parameters ---
POP_SIZE = 50
MAX_ITERS = 200
# The paper's best performing variant
VARIANT = 'ASM-Close-Global-Best'
# --- Run Optimization ---
optimizer = ASMCGO(
obj_func=sphere_objective,
constraint_func=sphere_constraint,
dim=DIMENSIONS,
pop_size=POP_SIZE,
max_iters=MAX_ITERS,
lb=LOWER_BOUND,
ub=UPPER_BOUND,
variant=VARIANT
)
best_solution, best_fitness, convergence_history = optimizer.optimize()
# --- Plotting Results (Optional) ---
try:
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.plot(convergence_history)
plt.title(f'Convergence Curve for {VARIANT}')
plt.xlabel('Iteration')
plt.ylabel('Best Penalized Fitness')
plt.grid(True)
plt.show()
except ImportError:
print("\nMatplotlib not found. Skipping plot.")
print("To plot results, please install it: pip install matplotlib")