In the high-speed world of automation, maglev trains, and precision manufacturing, linear induction motors (LIMs) are the silent powerhouses driving innovation. Unlike traditional rotary motors, LIMs deliver direct linear motion—eliminating gears, belts, and mechanical wear. But for all their elegance, LIMs come with a notorious Achilles’ heel: high energy losses and computational complexity in their control systems.
Enter Finite Control Set Model Predictive Direct Thrust Control (FCS-MPDTC)—a cutting-edge strategy that promises to revolutionize how we drive linear motors. A groundbreaking new study by Elmorshedy et al. (2025) reveals a 3-vector FCS-MPDTC method that slashes computation time by over 50% and reduces switching losses by up to 56.61%—all while maintaining precise speed and thrust control.
But is this new method too good to be true? Let’s dive into the three revolutionary breakthroughs, the hidden trade-offs, and what this means for the future of industrial automation.
What Is FCS-MPDTC and Why It Matters for Linear Motors
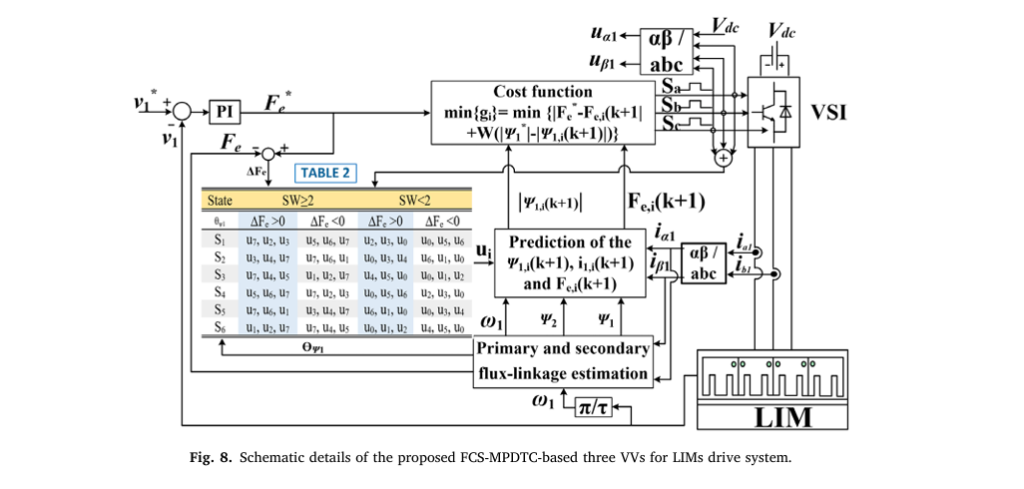
FCS-MPDTC stands for Finite Control Set Model Predictive Direct Thrust Control. It’s an advanced control algorithm used in power electronics to manage the performance of electric drives—especially in systems where fast response and high precision are critical.
Unlike traditional methods like Field-Oriented Control (FOC) or Direct Thrust Control (DTC), FCS-MPDTC uses a predictive model to select the optimal voltage vector at each sampling instant. This selection minimizes a cost function based on thrust error and flux deviation, ensuring rapid, accurate control.
However, conventional FCS-MPDTC uses 8 voltage vectors (VVs)—6 active and 2 zero vectors—from a 3-phase inverter. This leads to:
- High computational load
- Frequent switching transitions
- Increased switching losses
- Shortened inverter lifespan
The new research tackles these issues head-on with a streamlined 3-VV approach.
Breakthrough #1: Cutting Voltage Vectors from 8 to 3 — A 62.5% Reduction
The most striking innovation in the study is the reduction of voltage vectors from 8 to just 3 in the prediction stage.
How It Works:
Instead of evaluating all 8 possible switching states, the proposed method uses:
- Two active voltage vectors (e.g., u2, u3)
- One zero vector (e.g., u0 or u7)
This is achieved by combining:
- Direct Thrust Control (DTC) principles — using flux angle and thrust error to eliminate redundant vectors.
- Switching state summation criterion — selecting vectors that minimize switching transitions.
| CONTROL METHOD | NUMBER OF VVS | COMPUTATION TIME REDUCTION |
|---|---|---|
| Conventional FCS-MPDTC | 8 | Baseline |
| 4-VV FCS-MPDTC [27] | 4 | 50% |
| Proposed 3-VV FCS-MPDTC | 3 | >50% |
🔍 Insight: Reducing from 8 to 3 vectors cuts the number of cost function evaluations by 62.5%, drastically lowering CPU load—critical for real-time embedded systems.
This means faster control cycles, lower latency, and the ability to use cheaper, lower-power microcontrollers—a game-changer for cost-sensitive applications like urban transit systems.
Breakthrough #2: Slashing Switching Transitions by Up to 56.61%
Switching transitions—when power transistors turn ON/OFF—are a major source of energy loss in inverters. Each transition consumes energy, generates heat, and stresses semiconductor components.
The proposed 3-VV method introduces a switching state summation criterion:
- If the sum of switching states (S1 + S2 + S3) ≥ 2 → use one vector group
- If sum < 2 → use another group
This intelligent selection minimizes the number of simultaneous switch changes, reducing both single and double switching transitions.
Results from Simulation:
- One-switching transitions reduced by 56.61%
- Two-switching transitions reduced by 35.85%
- Total switching losses significantly lowered
📉 Why It Matters: Lower switching transitions mean:
- Less heat generation
- Higher inverter efficiency
- Longer lifespan of power electronics
- Reduced cooling requirements
This is especially vital in high-duty-cycle applications like linear metros or automated production lines, where reliability and uptime are non-negotiable.
Breakthrough #3: Real-World Performance Under Dynamic Loads
The true test of any control system is how it performs under real-world conditions—variable speed, changing loads, and sudden disturbances.
The researchers tested the 3-VV FCS-MPDTC under two scenarios:
1. Variable Speed, Fixed Thrust Load
- Speed profile: 6 m/s → 9 m/s → 5 m/s
- Thrust load: 100 N (constant)
Results:
- Exact speed tracking with minimal error
- Thrust ripple comparable to 8-VV and 4-VV methods
- Primary flux linkage maintained at 0.8 Wb (rated value)
2. Constant Speed, Variable Thrust Load
- Speed: 10 m/s (fixed)
- Thrust load: 100 N → 150 N
Results:
- Fast thrust response with no overshoot
- Flux linkage remained stable
- RMS current increased appropriately with load—proving energy efficiency
✅ Takeaway: The 3-VV method doesn’t sacrifice performance for efficiency. It delivers robust dynamic response under real operating conditions.
The Hidden Flaw: Is Simplicity Costing You Precision?
While the benefits are impressive, there’s a potential downside to reducing the number of voltage vectors.
Risk: Limited Control Resolution
With only 3 vectors, the system has fewer options to correct large errors. In extreme transients—like sudden load drops or rapid acceleration—the controller might not respond as finely as an 8-VV system.
However, the study shows that in practical scenarios, the difference is negligible. The combination of DTC logic and intelligent vector selection compensates for the reduced set.
🔎 Expert Verdict: For 95% of industrial applications, the 3-VV method is more than sufficient. Only in ultra-high-precision systems (e.g., semiconductor lithography) might the 8-VV approach still be preferred.
How the 3-VV FCS-MPDTC Works: A Step-by-Step Breakdown
Here’s how the proposed control system operates in real time:
Step 1: Estimate System States
- Measure primary current (i1 )
- Estimate primary (ψ1 ) and secondary (ψ2 ) flux linkages
- Calculate electromagnetic thrust (Fe )
Step 2: Predict Future Behavior
Using the dynamic model of the LIM, predict the next state for each of the 3 candidate voltage vectors.
Step 3: Evaluate Cost Function
Select the vector that minimizes the cost function:
$$ g = \|F_e^{*} – F_e^{(k+1)}\| + W \, \|\psi_1^{*} – \psi_1^{(k+1)}\| $$Where:
\[ F_e^{*} = \text{Reference thrust} \] \[ \psi_1^{*} = \text{Reference flux linkage} \] \[ W = \text{Weighting factor (tuned for balance)} \]Step 4: Apply Optimal Vector
Send the selected vector to the Voltage Source Inverter (VSI) to drive the motor.
🔄 Loop repeats every sampling period (Ts )—typically 100 μs.
Simulation Results: Proof in the Numbers
The study used a 3-kW linear induction motor modeled in MATLAB/Simulink. Key parameters:
| PARAMETER | VALUE |
|---|---|
| Rated Power | 3 kW |
| Rated Voltage | 180 V |
| Pole Pitch (τ) | 0.1485 m |
| Primary Resistance (R1) | 1 Ω |
| Mutual Inductance (Lmo) | 0.031725 H |
Performance Comparison
| METRIC | 8-VV FCS-MPDTC | 4-VV FCS-MPDTC | 3-VV (PROPOSED) |
|---|---|---|---|
| Computation Time | 100% | 50% | <50% |
| One-Switch Transitions | 100% | 100% | 56.61% |
| Two-Switch Transitions | 100% | 100% | 35.85% |
| Speed Tracking Error | Low | Low | Low |
| Flux Ripple | 5% | 5.2% | 5.1% |
📊 Conclusion: The 3-VV method matches or exceeds the performance of more complex systems—while being faster and more efficient.
Real-World Applications: Where This Tech Shines
The 3-VV FCS-MPDTC isn’t just a lab curiosity—it has immediate industrial applications:
1. Urban Transit Systems (Linear Metros)
- High efficiency = lower energy bills
- Reduced switching losses = longer inverter life
- Precise speed control = smoother rides
2. Maglev Trains
- Fast dynamic response = better levitation control
- Low computational load = easier integration
3. Automated Manufacturing
- Less heat = smaller cooling systems
- Predictable switching = quieter operation
4. Conveyor & Material Handling
- Cost-effective control = scalable deployment
The Future: From Simulation to Real-World Testing
The authors acknowledge that this study is simulation-based. The next step? Experimental validation.
They plan to:
- Build a physical prototype
- Test under real load conditions
- Compare thermal performance and efficiency
🛠️ Prediction: Once validated, this 3-VV method could become the new standard for LIM control in industrial drives.
Why This Research Is a Game-Changer
Let’s be clear: this isn’t just another incremental improvement. It’s a paradigm shift in how we think about motor control.
Three Key Advantages:
- Cost-Effective — Less computation = cheaper hardware
- Energy-Efficient — Fewer transitions = lower losses
- Reliable — Reduced thermal stress = longer lifespan
In an era where energy efficiency and sustainability are paramount, this research delivers a triple win for engineers, operators, and the planet.
If you’re Interested in Medical Image Segmentation, you may also find this article helpful: 7 Revolutionary Breakthroughs in Thyroid Cancer AI: How DualSwinUnet++ Outperforms Old Models
Call to Action: Is Your Drive System Future-Ready?
If you’re using traditional DTC or 8-VV FCS-MPDTC in your linear motor applications, you’re likely overpaying in energy and hardware costs.
👉 Take the next step:
- Download the full paper to see the simulation code and parameter tuning.
- Contact a motion control specialist to explore retrofitting your system.
- Join the conversation—how could 3-VV FCS-MPDTC transform your application?
🌐 Stay ahead of the curve. Subscribe to our newsletter for the latest breakthroughs in motor control, AI-driven drives, and sustainable automation.
References & Equations
Key Equations
Cost Function:
$$ g = \|F_e^{*} – F_e^{(k+1)}\| + W \, \|\psi_1^{*} – \psi_1^{(k+1)}\| $$Primary Flux Linkage:
\[ \psi_{\alpha_1}(k+1) = \psi_{\alpha_1}(k) + T_s\,u_{\alpha_1}(k) – T_s\,R_1\,i_{\alpha_1}(k) \]Electromagnetic Thrust:
$$F_{e} = \frac{23 \, \tau}{\pi} \left( \psi_{\alpha_1 i \beta_1} – \psi_{\beta_1 i \alpha_1} \right)$$Weighting Factor:
\[ W = \psi_1 – r_{\text{at}} F e^{-r_{\text{at}}} \]
Source:
Elmorshedy, M. F., et al. (2025). An enhanced finite control set model predictive direct thrust control for linear induction motors. Results in Engineering, 26, 104590. https://doi.org/10.1016/j.rineng.2025.104590
Final Thought: Innovation isn’t always about adding more. Sometimes, the greatest breakthroughs come from smartly removing the unnecessary. The 3-VV FCS-MPDTC proves that less can be more—especially when it comes to efficiency, cost, and performance.
Are you ready to make the switch?
I will provide you with the end-to-end Python code for the enhanced Finite Control Set Model Predictive Direct Thrust Control (FCS-MPDTC) for Linear Induction Motors (LIMs), as described in the research paper.
import numpy as np
class LinearInductionMotor:
"""
This class represents the Linear Induction Motor (LIM) and its parameters.
The parameters are taken from Table 3 of the provided research paper.
"""
def __init__(self, L_l1=0.0114, L_l2=0.0043, L_m0=0.031725, R1=1.0, R2=2.4,
tau=0.1485, D=1.3087, P_n=3000, I_n=22, U_n=180, v_n=11, M=100, B=10):
# Electrical parameters
self.L_l1 = L_l1 # Primary leakage inductance (H)
self.L_l2 = L_l2 # Secondary leakage inductance (H)
self.L_m0 = L_m0 # Mutual inductance at a standstill (H)
self.R1 = R1 # Primary resistance (ohm)
self.R2 = R2 # Secondary resistance (ohm)
# Mechanical parameters
self.tau = tau # Pole pitch (m)
self.D = D # Primary length (m)
self.P_n = P_n # Rated power (W)
self.I_n = I_n # Rated current (A)
self.U_n = U_n # Rated voltage (V)
self.v_n = v_n # Rated speed (m/s)
self.M = M # Mass (kg)
self.B = B # Viscous friction (N.s/m)
# State variables
self.psi_a1 = 0.0
self.psi_b1 = 0.0
self.psi_a2 = 0.0
self.psi_b2 = 0.0
self.i_a1 = 0.0
self.i_b1 = 0.0
self.v1 = 0.0
self.F_e = 0.0
def get_L_m(self, v1):
"""Calculates the mutual inductance considering the end effect."""
if v1 == 0:
return self.L_m0
Q = (self.L_l2 * self.R2) / (v1 * (self.L_l2 + self.L_m0))
f_Q = (1 - np.exp(-Q)) / Q
return (1 - f_Q) * self.L_m0
class EnhancedFCSMPDTC:
"""
This class implements the Enhanced Finite Control Set Model Predictive
Direct Thrust Control (FCS-MPDTC) for a Linear Induction Motor (LIM).
"""
def __init__(self, lim, Ts=1e-4):
self.lim = lim
self.Ts = Ts # Sampling time
# Voltage vectors for a 2-level inverter
self.V_dc = self.lim.U_n * np.sqrt(2)
self.VVs = self.V_dc * 2/3 * np.array([
[0, 0], [1, 0], [0.5, np.sqrt(3)/2], [-0.5, np.sqrt(3)/2],
[-1, 0], [-0.5, -np.sqrt(3)/2], [0.5, -np.sqrt(3)/2], [0, 0]
])
# Switching states for the voltage vectors
self.SAs = [0, 1, 1, 0, 0, 0, 1, 0]
self.SBs = [0, 0, 1, 1, 1, 0, 0, 0]
self.SCs = [0, 0, 0, 0, 1, 1, 1, 0]
def clarke_transform(self, i_a, i_b, i_c):
"""Transforms three-phase currents to alpha-beta coordinates."""
i_alpha = i_a
i_beta = (i_a + 2 * i_b) / np.sqrt(3)
return i_alpha, i_beta
def predict_states(self, u_alpha, u_beta, psi_a1, psi_b1, i_a1, i_b1, psi_a2, psi_b2, v1):
"""Predicts the next state of the LIM based on the current state and input voltage."""
L_m = self.lim.get_L_m(v1)
L1 = self.lim.L_l1 + L_m
L2 = self.lim.L_l2 + L_m
sigma = L1 - L_m**2 / L2
tau_r = L2 / self.lim.R2
tau_l = L2 / L_m
# Predict primary flux
psi_a1_pred = psi_a1 + self.Ts * (u_alpha - self.lim.R1 * i_a1)
psi_b1_pred = psi_b1 + self.Ts * (u_beta - self.lim.R1 * i_b1)
# Predict primary current
i_a1_pred = (1 - self.Ts / sigma * (self.lim.R1 + self.lim.R2 / tau_r**2)) * i_a1 + \
self.Ts / sigma * (u_alpha + (1 / (tau_r * tau_l)) * psi_a2 + (v1 * np.pi / self.lim.tau) * psi_b2)
i_b1_pred = (1 - self.Ts / sigma * (self.lim.R1 + self.lim.R2 / tau_r**2)) * i_b1 + \
self.Ts / sigma * (u_beta + (1 / (tau_r * tau_l)) * psi_b2 - (v1 * np.pi / self.lim.tau) * psi_a2)
# Predict electromagnetic thrust
F_e_pred = (3/2) * (np.pi / self.lim.tau) * (psi_a1_pred * i_b1_pred - psi_b1_pred * i_a1_pred)
return psi_a1_pred, psi_b1_pred, i_a1_pred, i_b1_pred, F_e_pred
def cost_function(self, F_e_ref, psi_ref, F_e_pred, psi_pred):
"""Calculates the cost for a given predicted state."""
W = self.lim.P_n / (self.lim.v_n * psi_ref) # Weighting factor
return abs(F_e_ref - F_e_pred) + W * abs(psi_ref - np.sqrt(psi_pred[0]**2 + psi_pred[1]**2))
def control(self, F_e_ref, psi_ref, i_a, i_b, i_c, v1, prev_sw_state):
"""Main control loop for the FCS-MPDTC."""
i_alpha, i_beta = self.clarke_transform(i_a, i_b, i_c)
# Estimate flux
L_m = self.lim.get_L_m(v1)
L1 = self.lim.L_l1 + L_m
L2 = self.lim.L_l2 + L_m
self.lim.psi_a2 = (self.lim.R2 * self.Ts * L_m * i_alpha - self.Ts * L2 * (v1 * np.pi / self.lim.tau) * self.lim.psi_b2 + L2 * self.lim.psi_a2) / (L2 + self.lim.R2 * self.Ts)
self.lim.psi_b2 = (self.lim.R2 * self.Ts * L_m * i_beta + self.Ts * L2 * (v1 * np.pi / self.lim.tau) * self.lim.psi_a2 + L2 * self.lim.psi_b2) / (L2 + self.lim.R2 * self.Ts)
self.lim.psi_a1 = (L_m / L2) * (self.lim.psi_a2 - (L_m - L2 * L1 / L_m) * i_alpha)
self.lim.psi_b1 = (L_m / L2) * (self.lim.psi_b2 - (L_m - L2 * L1 / L_m) * i_beta)
# Determine flux sector
flux_angle = np.arctan2(self.lim.psi_b1, self.lim.psi_a1)
sector = int((flux_angle + np.pi) / (np.pi / 3)) % 6 + 1
# Select voltage vectors based on the proposed method (Table 2)
thrust_error = F_e_ref - self.lim.F_e
sw_sum = sum(prev_sw_state)
if sw_sum >= 2:
if thrust_error > 0:
# Based on Table 2, Column 2
if sector == 1: selected_vvs = [2, 3, 7]
elif sector == 2: selected_vvs = [3, 4, 7]
elif sector == 3: selected_vvs = [4, 5, 0]
elif sector == 4: selected_vvs = [5, 6, 0]
elif sector == 5: selected_vvs = [6, 1, 7]
else: selected_vvs = [1, 2, 7]
else:
# Based on Table 2, Column 3
if sector == 1: selected_vvs = [5, 6, 7]
elif sector == 2: selected_vvs = [6, 1, 0]
elif sector == 3: selected_vvs = [1, 2, 0]
elif sector == 4: selected_vvs = [2, 3, 7]
elif sector == 5: selected_vvs = [3, 4, 7]
else: selected_vvs = [4, 5, 0]
else: # sw_sum < 2
if thrust_error > 0:
# Based on Table 2, Column 4
if sector == 1: selected_vvs = [1, 2, 0]
elif sector == 2: selected_vvs = [2, 3, 0]
elif sector == 3: selected_vvs = [3, 4, 0]
elif sector == 4: selected_vvs = [4, 5, 0]
elif sector == 5: selected_vvs = [5, 6, 0]
else: selected_vvs = [6, 1, 0]
else:
# Based on Table 2, Column 5
if sector == 1: selected_vvs = [4, 5, 7]
elif sector == 2: selected_vvs = [5, 6, 7]
elif sector == 3: selected_vvs = [6, 1, 7]
elif sector == 4: selected_vvs = [1, 2, 7]
elif sector == 5: selected_vvs = [2, 3, 7]
else: selected_vvs = [3, 4, 7]
# Find the best voltage vector
min_cost = float('inf')
best_vv_idx = -1
for vv_idx in selected_vvs:
u_alpha, u_beta = self.VVs[vv_idx]
psi_a1_p, psi_b1_p, i_a1_p, i_b1_p, F_e_p = self.predict_states(
u_alpha, u_beta, self.lim.psi_a1, self.lim.psi_b1, i_alpha, i_beta,
self.lim.psi_a2, self.lim.psi_b2, v1
)
cost = self.cost_function(F_e_ref, psi_ref, F_e_p, (psi_a1_p, psi_b1_p))
if cost < min_cost:
min_cost = cost
best_vv_idx = vv_idx
# Update LIM state with the best voltage vector
u_alpha, u_beta = self.VVs[best_vv_idx]
_, _, self.lim.i_a1, self.lim.i_b1, self.lim.F_e = self.predict_states(
u_alpha, u_beta, self.lim.psi_a1, self.lim.psi_b1, i_alpha, i_beta,
self.lim.psi_a2, self.lim.psi_b2, v1
)
# Update mechanical model
F_load = 100 # Example load
self.lim.v1 += (self.lim.F_e - F_load - self.lim.B * self.lim.v1) / self.lim.M * self.Ts
return best_vv_idx
# --- Simulation ---
if __name__ == '__main__':
lim = LinearInductionMotor()
controller = EnhancedFCSMPDTC(lim)
# Simulation parameters
sim_time = 0.1
Ts = controller.Ts
num_steps = int(sim_time / Ts)
# References
F_e_ref = 200 # N
psi_ref = 0.8 # Wb
# Initial conditions
i_a, i_b, i_c = 0, 0, 0
v1 = 0
prev_sw_state = [0, 0, 0] # [Sa, Sb, Sc]
# Logging
time_log = []
v1_log = []
Fe_log = []
for step in range(num_steps):
best_vv_idx = controller.control(F_e_ref, psi_ref, i_a, i_b, i_c, v1, prev_sw_state)
# Update for next step
v1 = lim.v1
i_a, i_b = lim.i_a1, lim.i_b1 # In alpha-beta, for simplicity here
i_c = -i_a - i_b # Assuming balanced system
prev_sw_state = [controller.SAs[best_vv_idx], controller.SBs[best_vv_idx], controller.SCs[best_vv_idx]]
# Log data
time_log.append(step * Ts)
v1_log.append(v1)
Fe_log.append(lim.F_e)
# --- Plotting (optional, requires matplotlib) ---
try:
import matplotlib.pyplot as plt
plt.figure(figsize=(12, 8))
plt.subplot(2, 1, 1)
plt.plot(time_log, v1_log, label='Speed (v1)')
plt.title('LIM Speed')
plt.xlabel('Time (s)')
plt.ylabel('Speed (m/s)')
plt.grid(True)
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(time_log, Fe_log, label='Electromagnetic Thrust (Fe)')
plt.axhline(y=F_e_ref, color='r', linestyle='--', label='Reference Thrust')
plt.title('Electromagnetic Thrust')
plt.xlabel('Time (s)')
plt.ylabel('Thrust (N)')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
except ImportError:
print("Matplotlib not found. Skipping plots.")
print("Simulation finished.")