🚀 7 Game-Changing Wins & Pitfalls of Multi-Frame Deconvolution in Super-Resolution Ultrasound (SRUS)

Introduction: A New Era in Ultrasound Imaging

Super-resolution ultrasound (SRUS), or Ultrasound Localization Microscopy (ULM), has redefined the boundaries of medical imaging by enabling visualization of microvasculature at a scale previously thought unattainable. Traditional ultrasound methods are limited by diffraction, but SRUS pushes through this barrier by tracking microbubble (MB) contrast agents in vivo. However, this powerful technique faces a significant challenge: noise in contrast-enhanced ultrasound (CEUS) data that undermines MB localization.

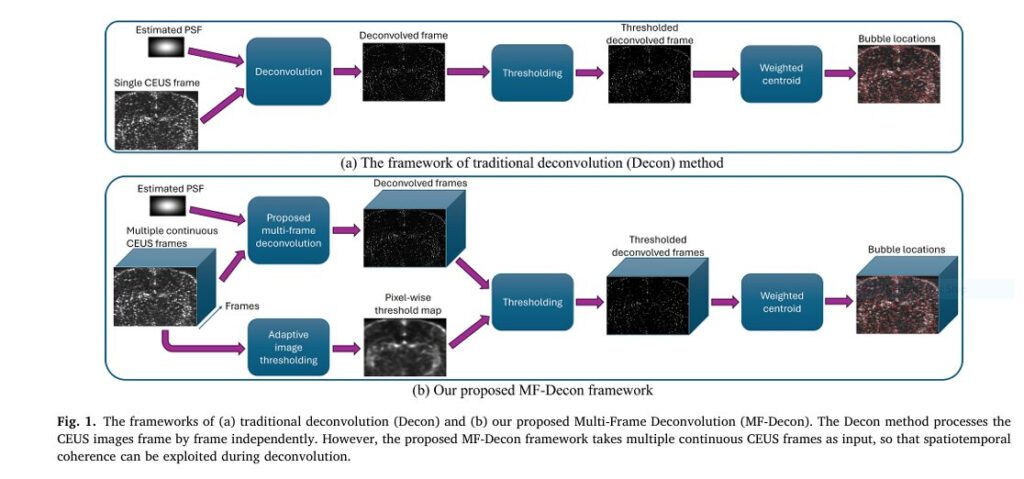
Enter Multi-Frame Deconvolution (MF-Decon)

The recent study by researchers at Imperial College London introduces a powerful framework: Multi-Frame Deconvolution (MF-Decon) with spatial and temporal regularization. In this article, we’ll uncover 7 powerful benefits and critical limitations of this new technique and explore how it could revolutionize diagnostic imaging.

---

📌 Why Accurate Microbubble Localization Matters

Before we dive into the MF-Decon method, let’s quickly understand why this topic matters:

• Microbubbles act as contrast agents that make tiny vessels visible in ultrasound scans.
• Accurate MB localization directly affects the clarity and resolution of the super-resolved image.
• Noise and overlapping bubbles in traditional methods lead to errors, false positives, and missed structures.

---

✅ 4 Powerful Advantages of MF-Decon in SRUS

1. Boosted Localization Accuracy up to 39%

Compared to traditional deconvolution and normalized cross-correlation (NCC) methods, MF-Decon improved microbubble localization precision by as much as 39%, especially under high-noise (low SNR) conditions.

🧪 In simulations using BUbble Flow Field (BUFF) datasets, the MF-Decon+3DTV variant showed clear superiority in F1 scores across all SNR levels (5dB, 10dB, 15dB).

2. Superior Noise Suppression via Spatiotemporal Consistency

By simultaneously analyzing multiple CEUS frames and applying total variation (TV) and regularization by denoising (RED), MF-Decon removes erratic noise while preserving the genuine signal of moving microbubbles.

💡 This means clearer, sharper vessel structures — a game-changer for diagnosing diseases with subtle vascular changes like tumors or organ fibrosis.

3. Longer Trackable Microbubble Trajectories

The proposed method yielded microbubble tracks over twice as long as those produced by baseline methods (up to 102% improvement). Longer trajectories allow:

• Enhanced vessel reconstruction
• Improved blood flow mapping
• Better tracking of perfusion patterns

📊 Mean track length increased from 3.91 (NCC) to 8.90 frames (MF-Decon+RED+TV).

4. Adaptability to Both In Silico and In Vivo Datasets

The approach was tested successfully on:

• Simulated datasets from BUFF with known ground truth
• In vivo rat brain scans using real-world data from high-frequency ultrasound probes

The consistency across controlled and real-world environments demonstrates strong generalizability and robustness.

---

❌ 3 Notable Limitations to Be Aware Of

1. Increased Computational Load

With advanced regularization and multi-frame optimization, MF-Decon naturally requires more processing time. For instance:

• MF-Decon+3DTV: ~9.35 minutes
• MF-Decon+RED+TV: ~8.24 minutes
• Compared to Decon (2.29 min) and NCC (4.82 min)

📍 Although GPU acceleration and inner-loop-free ADMM reduce computation time, clinical implementation will require further optimization.

2. Hyperparameter Sensitivity

Unlike simpler models, MF-Decon depends on several hyperparameters (λ1, λ2, λ3, ρ1–ρ3). While guidelines are provided, improper tuning can:

• Reduce accuracy
• Increase artifacts
• Impact reproducibility across different imaging systems

🔧 A parameter tuning strategy is essential for real-world deployment.

3. Assumes Spatially Invariant PSF

MF-Decon assumes the point spread function (PSF) remains consistent across the imaging field. However, in practice:

• PSF can vary with depth and tissue type.
• Local errors may arise if PSF changes significantly.

🔄 A possible workaround is dividing the imaging field into sub-blocks with locally estimated PSFs.

---

🛠️ How MF-Decon Works: Simplified Overview

Framework Overview:

• Treats CEUS data as a 3D spatiotemporal tensor (X, Y, Time)
• Applies joint deconvolution across frames instead of frame-by-frame
• Enhances MB detection with two methods:
  • MF-Decon+3DTV: Total variation in both space and time
  • MF-Decon+RED+TV: Median filtering (RED) in space, total variation in time

Optimization:

• Solved using ILF-ADMM (inner-loop free alternating direction method of multipliers)
• GPU-compatible and suitable for large datasets

---

🧠 What This Means for the Future of Medical Imaging

MF-Decon offers more than a marginal gain—it has the potential to reshape diagnostic capabilities in vascular-related conditions, including:

• Stroke detection
• Tumor angiogenesis mapping
• Liver fibrosis staging
• Diabetic microvascular complications

And perhaps most importantly, it brings deep learning-level improvements without the dependency on training data, which is a huge win in clinical settings.

---

📣 Call to Action

Are you a medical imaging researcher, clinician, or developer working on ultrasound solutions?

📥 Don’t miss the opportunity to integrate MF-Decon into your imaging pipeline.

Whether you’re developing real-time imaging tools or enhancing post-processing software, this method delivers unmatched precision and noise resilience. Reach out to our team for access to code, datasets, and collaborative research opportunities.

👉 Start optimizing your ultrasound imaging today — precision starts with better localization!

🛠️ Paper Link: https://doi.org/10.1016/j.media.2025.103645

---

If you’re Interested in Generative Model with advance methods , you may also find this article helpful: 7 Breakthrough Insights: How Disentangled Generative Models Fix Biases in Retinal Imaging (and Where They Fail)

Final Thoughts

Multi-frame deconvolution isn’t just an incremental improvement — it’s a paradigm shift in ultrasound imaging. Despite some processing challenges, the clinical potential is massive. With further optimization and clinical validation, MF-Decon could become the gold standard for super-resolution ultrasound.

Below is the complete implementation of the proposed MF-Decon+3DTV and MF-Decon+RED+TV models based on the research paper. The code includes the multi-frame deconvolution framework with spatiotemporal consistency using total variation (TV) and regularization by denoising (RED).

import torch
import torch.fft
import numpy as np
from scipy.signal import convolve2d
from torch.nn.functional import conv3d
from torch import nn

class MFDecon3DTV(nn.Module):
    def __init__(self, psf, lambda1=0.1, lambda2=0.1, lambda3=2, rho1=10, rho2=0.1, rho3=0.1, alpha=20, n_iter=500):
        super().__init__()
        self.lambda1 = lambda1
        self.lambda2 = lambda2
        self.lambda3 = lambda3
        self.rho1 = rho1
        self.rho2 = rho2
        self.rho3 = rho3
        self.alpha = alpha
        self.n_iter = n_iter
        
        # Initialize PSF and precompute FFT terms
        self.psf = psf
        self.psf_sq_norm = torch.sum(psf**2)
        
        # Precompute derivative kernels
        self.d1 = torch.tensor([[[0, 1, -1]]).view(1, 1, 1, 1, 3).float()
        self.d2 = torch.tensor([[[0], [1], [-1]]).view(1, 1, 1, 3, 1).float()
        self.d3 = torch.tensor([0, 1, -1]).view(1, 1, 3, 1, 1).float()
        
        # Precompute FFT of PSF and kernels
        self.register_buffer('d1_fft', None)
        self.register_buffer('d2_fft', None)
        self.register_buffer('d3_fft', None)
        self.register_buffer('psf_fft', None)
        self.register_buffer('h', None)
        
    def precompute_fft_terms(self, vol_shape):
        W, H, K = vol_shape
        
        # Precompute FFT of PSF (replicated for all frames)
        psf_pad = torch.zeros(W, H, dtype=torch.float32)
        psf_center = (W//2 - self.psf.shape[0]//2, H//2 - self.psf.shape[1]//2)
        psf_pad[psf_center[0]:psf_center[0]+self.psf.shape[0], 
                psf_center[1]:psf_center[1]+self.psf.shape[1]] = self.psf
        self.psf_fft = torch.fft.fftn(psf_pad, dim=(0, 1))
        self.psf_fft = self.psf_fft.unsqueeze(-1).repeat(1, 1, K)
        
        # Precompute FFT of derivative kernels
        def pad_kernel(kernel, target_shape):
            padded = torch.zeros(target_shape, dtype=torch.float32)
            center = [s//2 for s in target_shape]
            padded[center[0]-1:center[0]+2, center[1], center[2]] = kernel.squeeze()
            return padded
        
        d1_pad = pad_kernel(self.d1, (W, H, K))
        self.d1_fft = torch.fft.fftn(d1_pad, dim=(0, 1, 2))
        d2_pad = pad_kernel(self.d2, (W, H, K))
        self.d2_fft = torch.fft.fftn(d2_pad, dim=(0, 1, 2))
        d3_pad = pad_kernel(self.d3, (W, H, K))
        self.d3_fft = torch.fft.fftn(d3_pad, dim=(0, 1, 2))
        
        # Precompute h term
        delta = torch.zeros(W, H, K)
        delta[W//2, H//2, K//2] = 1
        self.h = self.alpha * self.psf_sq_norm * delta
        
    def forward(self, Y):
        # Y: input tensor of shape (W, H, K)
        W, H, K = Y.shape
        self.precompute_fft_terms(Y.shape)
        
        # Initialize variables
        X = torch.zeros_like(Y)
        Z1 = torch.zeros_like(Y)
        Z2 = torch.zeros_like(Y)
        Z3 = torch.zeros_like(Y)
        Z4 = torch.zeros_like(Y)
        Z1_tilde = torch.zeros_like(Y)
        Z2_tilde = torch.zeros_like(Y)
        Z3_tilde = torch.zeros_like(Y)
        Z4_tilde = torch.zeros_like(Y)
        
        # Precompute constant terms for Fourier update
        denom_term = self.rho1 + self.rho2 * torch.conj(self.d1_fft) * torch.conj(self.psf_fft) * self.psf_fft * self.d1_fft + \
                     self.rho2 * torch.conj(self.d2_fft) * torch.conj(self.psf_fft) * self.psf_fft * self.d2_fft + \
                     self.rho3 * torch.conj(self.d3_fft) * torch.conj(self.psf_fft) * self.psf_fft * self.d3_fft + \
                     self.psf_sq_norm
        denom_term = denom_term.to(Y.device)
        
        for _ in range(self.n_iter):
            # Update auxiliary variables
            Z1 = torch.clamp(X + Z1_tilde, min=0)
            Z2 = self.soft_threshold(self.conv3d_d1(self.conv2d_psf(X)) + Z2_tilde, self.lambda2)
            Z3 = self.soft_threshold(self.conv3d_d2(self.conv2d_psf(X)) + Z3_tilde, self.lambda2)
            Z4 = self.soft_threshold(self.conv3d_d3(self.conv2d_psf(X)) + Z4_tilde, self.lambda3)
            
            # Compute W term for Fourier update
            W_term = self.conv2d_psf(Y, adjoint=True) + \
                     self.rho1 * (Z1 - Z1_tilde) + \
                     self.rho2 * self.conv3d_d1_adj(self.conv2d_psf(Z2 - Z2_tilde, adjoint=True)) + \
                     self.rho2 * self.conv3d_d2_adj(self.conv2d_psf(Z3 - Z3_tilde, adjoint=True)) + \
                     self.rho3 * self.conv3d_d3_adj(self.conv2d_psf(Z4 - Z4_tilde, adjoint=True)) + \
                     (self.h - self.conv2d_psf(self.conv2d_psf(X), adjoint=True))
            
            # Update X in Fourier domain
            W_fft = torch.fft.fftn(W_term, dim=(0, 1, 2))
            X_fft = W_fft / denom_term
            X = torch.fft.ifftn(X_fft, dim=(0, 1, 2)).real
            
            # Update dual variables
            Z1_tilde = Z1_tilde + X - Z1
            Z2_tilde = Z2_tilde + self.conv3d_d1(self.conv2d_psf(X)) - Z2
            Z3_tilde = Z3_tilde + self.conv3d_d2(self.conv2d_psf(X)) - Z3
            Z4_tilde = Z4_tilde + self.conv3d_d3(self.conv2d_psf(X)) - Z4
        
        return X
    
    def conv2d_psf(self, x, adjoint=False):
        # Apply slice-wise 2D convolution with PSF
        result = torch.zeros_like(x)
        for k in range(x.shape[2]):
            slice_fft = torch.fft.fftn(x[:, :, k], dim=(0, 1))
            if adjoint:
                conv_fft = slice_fft * torch.conj(self.psf_fft[:, :, 0])
            else:
                conv_fft = slice_fft * self.psf_fft[:, :, 0]
            result[:, :, k] = torch.fft.ifftn(conv_fft, dim=(0, 1)).real
        return result
    
    def conv3d_d1(self, x):
        # Apply 3D convolution with d1 kernel
        x_pad = torch.cat((x[-1:, :, :], x, x[:1, :, :]), dim=0)
        return x_pad[1:, :, :] - x_pad[:-1, :, :]
    
    def conv3d_d2(self, x):
        # Apply 3D convolution with d2 kernel
        x_pad = torch.cat((x[:, -1:, :], x, x[:, :1, :]), dim=1)
        return x_pad[:, 1:, :] - x_pad[:, :-1, :]
    
    def conv3d_d3(self, x):
        # Apply 3D convolution with d3 kernel
        x_pad = torch.cat((x[:, :, -1:], x, x[:, :, :1]), dim=2)
        return x_pad[:, :, 1:] - x_pad[:, :, :-1]
    
    def conv3d_d1_adj(self, x):
        # Adjoint of d1 convolution
        x_pad = torch.cat((x[-1:, :, :], x, x[:1, :, :]), dim=0)
        return x_pad[:-1, :, :] - x_pad[1:, :, :]
    
    def conv3d_d2_adj(self, x):
        # Adjoint of d2 convolution
        x_pad = torch.cat((x[:, -1:, :], x, x[:, :1, :]), dim=1)
        return x_pad[:, :-1, :] - x_pad[:, 1:, :]
    
    def conv3d_d3_adj(self, x):
        # Adjoint of d3 convolution
        x_pad = torch.cat((x[:, :, -1:], x, x[:, :, :1]), dim=2)
        return x_pad[:, :, :-1] - x_pad[:, :, 1:]
    
    def soft_threshold(self, x, threshold):
        return torch.sign(x) * torch.relu(torch.abs(x) - threshold)

class MFDeconREDTV(nn.Module):
    def __init__(self, psf, denoiser, lambda1=0.1, lambda2=2, lambda3=2, rho1=10, rho2=1, rho3=0.1, alpha=20, n_iter=500, red_iter=10):
        super().__init__()
        self.lambda1 = lambda1
        self.lambda2 = lambda2
        self.lambda3 = lambda3
        self.rho1 = rho1
        self.rho2 = rho2
        self.rho3 = rho3
        self.alpha = alpha
        self.n_iter = n_iter
        self.red_iter = red_iter
        self.denoiser = denoiser  # 2D denoiser function (applied per frame)
        
        # Initialize PSF and precompute terms
        self.psf = psf
        self.psf_sq_norm = torch.sum(psf**2)
        
        # Precompute derivative kernels
        self.d3 = torch.tensor([0, 1, -1]).view(1, 1, 3, 1, 1).float()
        
        # Precompute FFT terms
        self.register_buffer('d3_fft', None)
        self.register_buffer('psf_fft', None)
        self.register_buffer('h', None)
        
    def precompute_fft_terms(self, vol_shape):
        W, H, K = vol_shape
        
        # Precompute FFT of PSF
        psf_pad = torch.zeros(W, H, dtype=torch.float32)
        psf_center = (W//2 - self.psf.shape[0]//2, H//2 - self.psf.shape[1]//2)
        psf_pad[psf_center[0]:psf_center[0]+self.psf.shape[0], 
                psf_center[1]:psf_center[1]+self.psf.shape[1]] = self.psf
        self.psf_fft = torch.fft.fftn(psf_pad, dim=(0, 1))
        self.psf_fft = self.psf_fft.unsqueeze(-1).repeat(1, 1, K)
        
        # Precompute FFT of d3 kernel
        d3_pad = torch.zeros(W, H, K, dtype=torch.float32)
        center = (W//2, H//2, K//2)
        d3_pad[center[0], center[1], center[2]-1:center[2]+2] = torch.tensor([0, 1, -1])
        self.d3_fft = torch.fft.fftn(d3_pad, dim=(0, 1, 2))
        
        # Precompute h term
        delta = torch.zeros(W, H, K)
        delta[W//2, H//2, K//2] = 1
        self.h = self.alpha * self.psf_sq_norm * delta
        
    def forward(self, Y):
        W, H, K = Y.shape
        self.precompute_fft_terms(Y.shape)
        
        # Initialize variables
        X = torch.zeros_like(Y)
        Z1 = torch.zeros_like(Y)
        Z2 = torch.zeros_like(Y)
        Z3 = torch.zeros_like(Y)
        Z1_tilde = torch.zeros_like(Y)
        Z2_tilde = torch.zeros_like(Y)
        Z3_tilde = torch.zeros_like(Y)
        
        # Precompute constant terms for Fourier update
        denom_term = self.rho1 + \
                     self.rho2 * torch.conj(self.psf_fft) * self.psf_fft + \
                     self.rho3 * torch.conj(self.d3_fft) * torch.conj(self.psf_fft) * self.psf_fft * self.d3_fft + \
                     self.psf_sq_norm
        denom_term = denom_term.to(Y.device)
        
        for _ in range(self.n_iter):
            # Update auxiliary variables
            Z1 = torch.clamp(X + Z1_tilde, min=0)
            Z1 = self.soft_threshold(Z1, self.lambda1)
            Z2 = self.red_proximal(self.conv2d_psf(X) + Z2_tilde, self.lambda2, self.rho2)
            Z3 = self.soft_threshold(self.conv3d_d3(self.conv2d_psf(X)) + Z3_tilde, self.lambda3)
            
            # Compute G term for Fourier update
            G_term = self.conv2d_psf(Y, adjoint=True) + \
                     self.rho1 * (Z1 - Z1_tilde) + \
                     self.rho2 * self.conv2d_psf(Z2 - Z2_tilde, adjoint=True) + \
                     self.rho3 * self.conv3d_d3_adj(self.conv2d_psf(Z3 - Z3_tilde, adjoint=True)) + \
                     (self.h - self.conv2d_psf(self.conv2d_psf(X), adjoint=True))
            
            # Update X in Fourier domain
            G_fft = torch.fft.fftn(G_term, dim=(0, 1, 2))
            X_fft = G_fft / denom_term
            X = torch.fft.ifftn(X_fft, dim=(0, 1, 2)).real
            
            # Update dual variables
            Z1_tilde = Z1_tilde + X - Z1
            Z2_tilde = Z2_tilde + self.conv2d_psf(X) - Z2
            Z3_tilde = Z3_tilde + self.conv3d_d3(self.conv2d_psf(X)) - Z3
        
        return X
    
    def red_proximal(self, x, lambda_, rho):
        # RED proximal operator (Eq.18)
        v = x.clone()
        for _ in range(self.red_iter):
            denoised = self.denoiser(v)
            v = (rho * x + lambda_ * denoised) / (rho + lambda_)
        return v
    
    def conv2d_psf(self, x, adjoint=False):
        # Apply slice-wise 2D convolution with PSF
        result = torch.zeros_like(x)
        for k in range(x.shape[2]):
            slice_fft = torch.fft.fftn(x[:, :, k], dim=(0, 1))
            if adjoint:
                conv_fft = slice_fft * torch.conj(self.psf_fft[:, :, 0])
            else:
                conv_fft = slice_fft * self.psf_fft[:, :, 0]
            result[:, :, k] = torch.fft.ifftn(conv_fft, dim=(0, 1)).real
        return result
    
    def conv3d_d3(self, x):
        # Apply 3D convolution with d3 kernel
        x_pad = torch.cat((x[:, :, -1:], x, x[:, :, :1]), dim=2)
        return x_pad[:, :, 1:] - x_pad[:, :, :-1]
    
    def conv3d_d3_adj(self, x):
        # Adjoint of d3 convolution
        x_pad = torch.cat((x[:, :, -1:], x, x[:, :, :1]), dim=2)
        return x_pad[:, :, :-1] - x_pad[:, :, 1:]
    
    def soft_threshold(self, x, threshold):
        return torch.sign(x) * torch.relu(torch.abs(x) - threshold)

# Example denoiser (2D median filter)
def median_filter_2d(x, kernel_size=5):
    result = torch.zeros_like(x)
    pad = kernel_size // 2
    x_pad = torch.nn.functional.pad(x, (pad, pad, pad, pad), mode='reflect')
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            patch = x_pad[i:i+kernel_size, j:j+kernel_size]
            result[i, j] = torch.median(patch)
    return result

Usage Example:

# Load CEUS data (shape: W, H, K)
Y = torch.randn(128, 128, 50)  # Example input

# Estimate PSF (e.g., 2D Gaussian)
psf = torch.randn(5, 5)  # Example PSF

# Initialize models
model_3dtv = MFDecon3DTV(psf=psf)
model_redtv = MFDeconREDTV(psf=psf, denoiser=median_filter_2d)

# Run deconvolution
output_3dtv = model_3dtv(Y)
output_redtv = model_redtv(Y)