Balancing the Tension: How a New AI Strategy Solves the Hidden Conflict in Semi-Supervised Image Segmentation

In the rapidly evolving world of artificial intelligence, one of the most significant challenges is teaching machines to understand images with minimal human supervision. This is where semi-supervised semantic segmentation comes in—a powerful technique that aims to accurately label every pixel in an image using only a small amount of manually annotated data alongside a vast pool of unlabeled images. While this approach promises to drastically reduce the cost and time associated with creating large, labeled datasets, a critical, often overlooked problem has been hindering its full potential: optimization conflict.

This article dives deep into a groundbreaking new research paper presented at ICCV 2025, titled “Two Losses, One Goal: Balancing Conflict Gradients for Semi-supervised Semantic Segmentation.” We’ll break down the core problem, explain the innovative solution proposed by researchers from Tsinghua University and the University of Science and Technology of China, and explore how their method, called the Pareto Optimization Strategy (POS), is set to revolutionize this field. By the end, you’ll understand not just what the problem is, but why it matters and how this new strategy paves the way for more accurate, robust, and efficient AI models.

The Core Challenge: When Two Learning Goals Collide

Imagine training a neural network to identify objects in photos—like distinguishing a person from a car or a tree from the sky. In a fully supervised scenario, you’d need millions of images where every single pixel is meticulously labeled by a human. This is incredibly expensive and time-consuming.

Semi-supervised learning offers a smarter path. It combines a small set of these perfectly labeled images with a much larger set of unlabeled ones. The model learns from the labeled data and then uses its own predictions on the unlabeled data to refine itself. This is typically done using a “teacher-student” framework, where a “teacher” network generates pseudo-labels for the unlabeled data, which are then used to train the “student” network.

The student network is guided by two distinct objectives:

Supervised Loss (L_sup): Minimizing the error between its predictions and the true, ground-truth labels for the small labeled dataset.
Unsupervised Loss (L_unsup): Minimizing the difference between its predictions on strongly augmented versions of unlabeled images and the pseudo-labels generated by the teacher network on weakly augmented versions of the same images.

This setup sounds logical, but here’s the hidden flaw: these two objectives can pull the model’s parameters in opposite directions during training. Think of it like two people trying to steer a car—one wants to turn left, the other wants to turn right. If you simply average their steering inputs, you might end up going straight, but neither driver’s goal is truly satisfied, and the car could become unstable.

The authors of the ICCV 2025 paper identified this as a major, under-explored issue. They conducted an analysis on the popular Pascal VOC dataset and found that the gradients—the mathematical vectors indicating the direction and magnitude of change needed to minimize each loss—are often negatively correlated. In simple terms, improving performance on one objective can actively hurt performance on the other.

Key Takeaway: The fundamental problem isn’t a lack of data or a poor algorithm; it’s a built-in optimization conflict between the supervised and unsupervised learning signals. Traditional methods that naively sum these losses with equal weights are inherently flawed.

Introducing the Pareto Optimization Strategy (POS): A Mathematical Solution to a Real-World Problem

So, how do you resolve this tug-of-war? The researchers propose a novel solution inspired by game theory and multi-objective optimization: the Pareto Optimization Strategy (POS).

Instead of forcing the model to follow a single, fixed combination of gradients, POS dynamically calculates the optimal weighting for each gradient at every training step. Its goal is to find a single, unified descent direction that benefits both objectives simultaneously, effectively harmonizing them into “one goal.”

Here’s how it works mathematically. At each iteration, the model computes two gradients:

g_s^S: The gradient from the supervised loss for the current mini-batch S.
g_u^S: The gradient from the unsupervised loss for the same mini-batch S.

POS then solves the following optimization problem:

\[ \min_{\alpha_s, \alpha_u \in \mathbb{R}} \| \alpha_s g_s^S + \alpha_u g_u^S \|_2 \\ \text{s.t. } \alpha_s, \alpha_u \geq 0, \quad \alpha_s + \alpha_u = 1 \]

This equation seeks to find the weights α_s and α_u that produce a combined gradient vector with the smallest possible length (minimum norm) while ensuring both weights are non-negative and sum to one. The solution to this problem is elegant and has a closed-form analytical formula, making it computationally efficient to implement.

The result is a dynamically weighted integrated gradient α_sg^S + α_ug^S. Crucially, this integrated gradient is guaranteed to have a non-negative cosine similarity with both the original supervised and unsupervised gradients. This means it points in a direction that is beneficial for both learning tasks, eliminating the destructive conflict.

Key Takeaway: POS doesn’t just compromise; it finds the best possible path forward that advances both learning goals. It transforms a conflicting dual-objective problem into a coherent, unified optimization process.

Why Dynamic Weighting Beats Fixed Ratios: The Power of Adaptability

Previous methods, which we can call the “uniform strategy,” typically assign a fixed weight ratio (e.g., 50/50) to the supervised and unsupervised losses. This approach is simple but brittle. It fails to account for the fact that the relationship between the two losses changes throughout the training process. Sometimes the supervised signal is stronger, sometimes the unsupervised signal provides more useful information.

POS, by contrast, is adaptive. It constantly reassesses the learning status of the model and adjusts the weights accordingly. The paper’s analysis reveals a fascinating insight: POS consistently assigns a larger weight to the unsupervised gradient.

Why is this? The researchers provide a compelling explanation based on gradient magnitude and sampling noise. Their experiments show that the gradient from the supervised loss tends to be significantly larger in magnitude and has higher variance (covariance) than the gradient from the unsupervised loss. This is because training on true, labeled data is inherently more challenging and noisy than training on pseudo-labels generated by a similar model.

By assigning more weight to the smaller, less noisy unsupervised gradient, POS helps to stabilize the training process. It prevents the model from being overly dominated by the potentially erratic supervised signal, leading to smoother convergence and better overall performance.

\[\text{If } \cos(\beta) \geq\frac{\|g_u^S\|}{\|g_s^S\|}, \text{ then } \alpha_u > \alpha_s\]

This dynamic adjustment is what sets POS apart. It’s not a static rule; it’s a responsive system that intelligently balances the two learning signals based on their current state.

Key Takeaway: The “more is better” mentality doesn’t apply here. Sometimes, giving more weight to the smaller, steadier signal leads to a more robust and effective model.

Enhancing Performance Further: The Magnitude Enhancement Operation (MEO)

While POS effectively resolves the directional conflict between gradients, the researchers discovered another subtle issue. Their analysis suggests that POS, despite its superior performance, might lead the model to converge to a “sharp minimum.” In machine learning, sharp minima are associated with poorer generalization—the model performs well on the training data but may falter when faced with new, unseen data.

To address this, they introduced a second component: the Magnitude Enhancement Operation (MEO). MEO takes the conflict-free direction provided by POS and enhances its magnitude. Specifically, it scales the POS-integrated gradient to match the magnitude of the gradient produced by the traditional uniform strategy.

\[ h_{POS}^S = \left( \alpha_u g_u^S + \alpha_s g_s^S \right) \cdot\frac{ \left\| \frac{1}{2} g_u^S + \frac{1}{2} g_s^S \right\| }{ \left\| \alpha_u g_u^S + \alpha_s g_s^S \right\| } \]

This scaling increases the “noise strength” during training, which, counterintuitively, helps the model escape sharp minima and find a “flatter minimum.” Flatter minima are known to correlate with better generalization, meaning the model will be more robust and accurate in real-world applications.

Think of it like this: POS gives you the right direction to walk. MEO gives you a stronger stride, helping you navigate the landscape more effectively and avoid getting stuck in a shallow, misleading valley.

Key Takeaway: Combining POS with MEO creates a synergistic effect. You get the benefit of a conflict-free direction and enhanced generalization, leading to state-of-the-art performance.

Proven Results: Superior Performance Across Benchmarks

The true test of any new AI method is its performance on real-world benchmarks. The researchers rigorously tested their combined POS+MEO strategy by integrating it into two leading semi-supervised segmentation frameworks: UniMatch V1 (using a CNN backbone) and UniMatch V2 (using a Transformer backbone).

The results were consistently impressive across three major datasets:

COCO Dataset (Challenging 81-Class Object Segmentation)

METHOD	1/512 SPLIT	1/256 SPLIT
UniMatch V1	31.9	38.9
UniMatch V1 + Ours	34.0	40.3
UniMatch V2	39.3	45.4
UniMatch V2 + Ours	40.9	46.8

On the extremely sparse 1/512 split, their method boosted performance by 2.1% and 1.6% for the two architectures, respectively.

PASCAL VOC Dataset (Classic 20-Class Segmentation)

METHOD	1/16 SPLIT (92 IMAGES)	FULL DATASET
UniMatch V1	75.2	81.2
UniMatch V1 + Ours	77.6	81.9
UniMatch V2	79.0	87.8
UniMatch V2 + Ours	80.7	88.3

In the most label-scarce scenario (only 92 labeled images), their method achieved a remarkable 2.4% mIoU improvement over the baseline.

Cityscapes Dataset (Urban Scene Understanding)

METHOD	1/6 SPLIT	1/8 SPLIT
UniMatch V1	76.6	77.9
UniMatch V1 + Ours	77.6	78.5
UniMatch V2	80.6	81.9
UniMatch V2 + Ours	81.4	82.7

Even on the complex Cityscapes dataset, the improvements were consistent, proving the method’s robustness.

These results demonstrate that the POS+MEO strategy is not a niche trick; it’s a broadly applicable enhancement that delivers significant gains across different data splits, model architectures (CNNs and Transformers), and benchmark datasets.

Key Takeaway: The proposed method is not just theoretically sound; it delivers tangible, state-of-the-art improvements in practical, real-world scenarios.

Visualizing the Impact: From Theory to Practice

The paper includes several insightful visualizations that help illustrate the power of their approach.

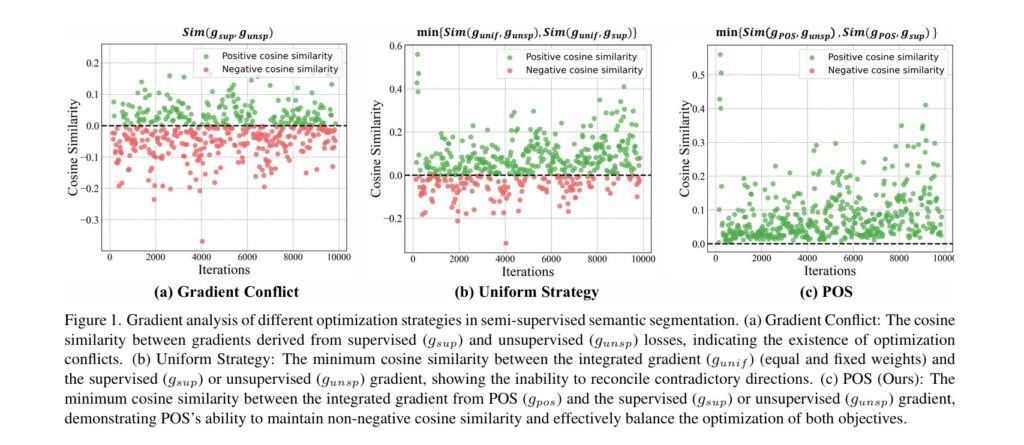
Figure 1: Gradient Conflict Analysis
- Image Description: This figure compares three strategies. Part (a) shows a negative cosine similarity between supervised and unsupervised gradients, confirming the existence of conflict. Part (b) shows that the uniform strategy often produces an integrated gradient that is still negatively correlated with one of the original gradients. Part (c) demonstrates that the POS strategy maintains a non-negative cosine similarity with both gradients, visually proving its ability to balance the conflict.

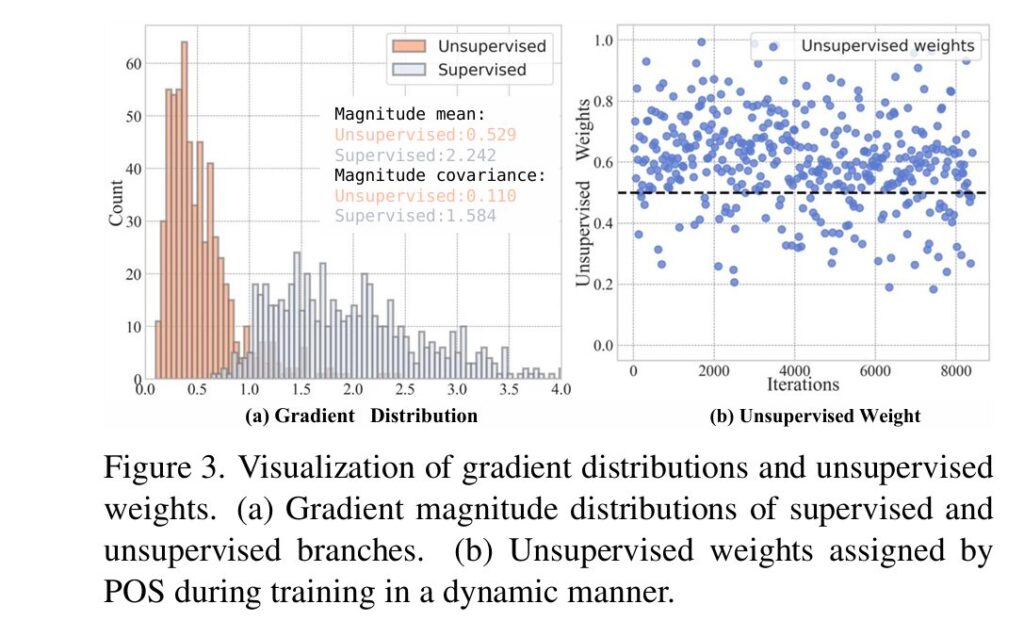
Figure 3: Gradient Distributions and Dynamic Weights
- Image Description: Part (a) is a bar chart showing the mean and covariance of gradient magnitudes. It clearly shows the unsupervised gradient has a much smaller magnitude (mean 0.529 vs. 2.242) and lower covariance (0.110 vs. 1.584). Part (b) is a line graph plotting the unsupervised weight α_u assigned by POS over training iterations, showing it consistently stays above 0.5.

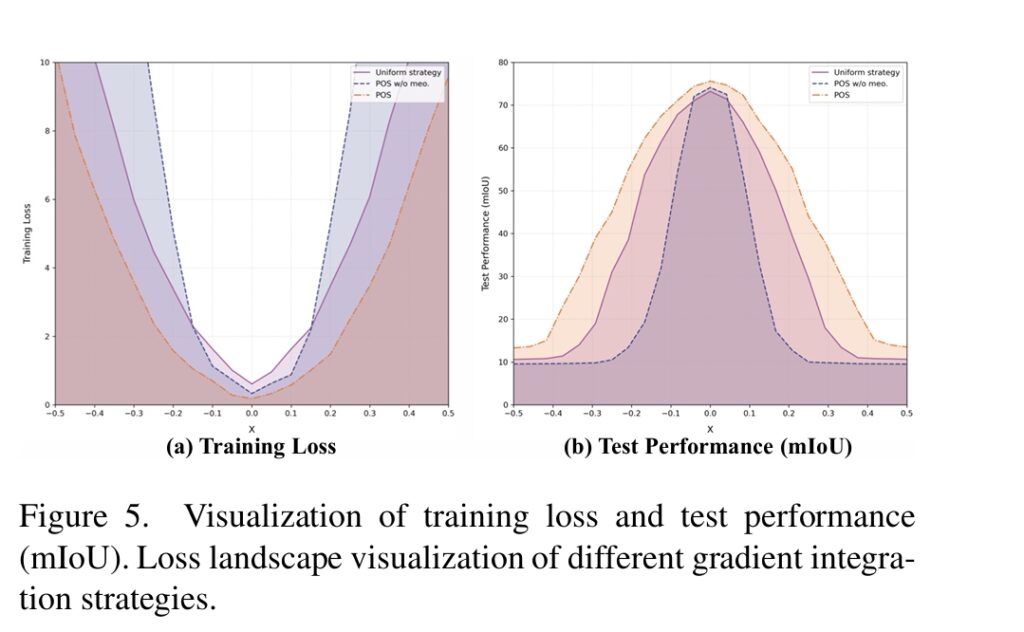
Figure 5: Loss Landscape Visualization
- Image Description: These 3D plots visualize the “loss landscape” around the optimal point. The uniform strategy shows a narrow, sharp peak. The POS strategy without MEO is flatter. The POS+MEO strategy shows the widest, flattest basin, indicating superior generalization.

Conclusion: A New Standard for Efficient AI Training

The research presented in this ICCV 2025 paper represents a significant leap forward in semi-supervised semantic segmentation. By identifying and directly addressing the fundamental optimization conflict between supervised and unsupervised learning objectives, the authors have developed a powerful and elegant solution.

The Pareto Optimization Strategy (POS) provides a mathematically grounded method for dynamically balancing these conflicting gradients, ensuring that the model’s training is always moving in a direction that benefits both learning goals. The Magnitude Enhancement Operation (MEO) further refines this by promoting convergence to flatter, more generalizable minima.

The implications are far-reaching. This work not only improves the accuracy of existing models but also provides a new framework for thinking about multi-objective optimization in AI. It highlights the importance of understanding the underlying dynamics of the training process rather than relying on heuristic rules.

For developers and researchers working on computer vision, this method offers a simple, plug-and-play enhancement that can be integrated into existing pipelines to achieve immediate performance boosts. For businesses looking to deploy AI for tasks like autonomous driving, medical imaging, or satellite analysis, this research brings us closer to building highly accurate models with far less reliance on costly, manual data labeling.

What do you think? Does this approach of dynamically balancing conflicting objectives have applications beyond image segmentation? Share your thoughts in the comments below, and let’s discuss how this innovation might shape the future of AI!

Read & Download the full Paper here.

Below is the complete self-contained PyTorch implementation of the paper’s core contribution: the Pareto Optimization Strategy (POS) and the Magnitude Enhancement Operation (MEO).

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.utils.data as data
from torch.utils.data import DataLoader
from collections.abc import Iterable
import copy
import warnings

# Suppress user warnings (e.g., from upsampling)
warnings.filterwarnings("ignore", category=UserWarning)

# --- Constants ---
IMG_SIZE = 128
NUM_CLASSES = 21
BATCH_SIZE_L = 4
BATCH_SIZE_U = 8
CONFIDENCE_THRESHOLD = 0.7
IGNORE_INDEX = 255
EMA_ALPHA = 0.999
LEARNING_RATE = 1e-3
EPOCHS = 5
STEPS_PER_EPOCH = 50

# --- 1. Helper Functions ---

def flatten_gradients(grads: Iterable[torch.Tensor]) -> torch.Tensor:
    """Flattens a list of gradient tensors into a single 1D vector."""
    return torch.cat([g.reshape(-1) for g in grads if g is not None])

@torch.no_grad()
def update_teacher_model(student_model: nn.Module, teacher_model: nn.Module, alpha: float):
    """Exponential Moving Average update for the teacher model."""
    for teacher_param, student_param in zip(teacher_model.parameters(), student_model.parameters()):
        teacher_param.data.mul_(alpha).add_(student_param.data, alpha=1 - alpha)

# --- 2. DeepLabv3+ Model Architecture ---

class ASPP(nn.Module):
    """Atrous Spatial Pyramid Pooling (ASPP)"""
    def __init__(self, in_channels, out_channels):
        super(ASPP, self).__init__()
        dilations = [1, 6, 12, 18]
        
        self.conv1x1 = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, 1, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU()
        )
        self.conv_d6 = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, 3, padding=dilations[1], dilation=dilations[1], bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU()
        )
        self.conv_d12 = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, 3, padding=dilations[2], dilation=dilations[2], bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU()
        )
        self.conv_d18 = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, 3, padding=dilations[3], dilation=dilations[3], bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU()
        )
        
        self.global_avg_pool = nn.Sequential(
            nn.AdaptiveAvgPool2d((1, 1)),
            nn.Conv2d(in_channels, out_channels, 1, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU()
        )
        
        self.conv1x1_out = nn.Sequential(
            nn.Conv2d(out_channels * 5, out_channels, 1, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU()
        )

    def forward(self, x):
        size = x.shape[2:]
        
        c1 = self.conv1x1(x)
        c6 = self.conv_d6(x)
        c12 = self.conv_d12(x)
        c18 = self.conv_d18(x)
        
        c_pool = self.global_avg_pool(x)
        c_pool = F.interpolate(c_pool, size=size, mode='bilinear', align_corners=False)
        
        out = torch.cat([c1, c6, c12, c18, c_pool], dim=1)
        out = self.conv1x1_out(out)
        return out

class DeepLabv3Plus(nn.Module):
    """Simplified DeepLabv3+ for demonstration."""
    def __init__(self, in_channels=3, num_classes=21):
        super(DeepLabv3Plus, self).__init__()
        # Simplified "backbone" (just a few conv layers)
        self.backbone = nn.Sequential(
            nn.Conv2d(in_channels, 64, 3, padding=1, bias=False), nn.BatchNorm2d(64), nn.ReLU(),
            nn.Conv2d(64, 128, 3, padding=1, stride=2, bias=False), nn.BatchNorm2d(128), nn.ReLU(),
            nn.Conv2d(128, 256, 3, padding=1, stride=2, bias=False), nn.BatchNorm2d(256), nn.ReLU(),
            nn.Conv2d(256, 512, 3, padding=1, bias=False), nn.BatchNorm2d(512), nn.ReLU(),
        )
        
        # Low-level features from backbone
        self.low_level_conv = nn.Sequential(
            nn.Conv2d(128, 48, 1, bias=False),
            nn.BatchNorm2d(48),
            nn.ReLU()
        )
        
        self.aspp = ASPP(512, 256)
        
        # Decoder
        self.decoder = nn.Sequential(
            nn.Conv2d(256 + 48, 256, 3, padding=1, bias=False),
            nn.BatchNorm2d(256),
            nn.ReLU(),
            nn.Conv2d(256, 256, 3, padding=1, bias=False),
            nn.BatchNorm2d(256),
            nn.ReLU(),
            nn.Conv2d(256, num_classes, 1)
        )

    def forward(self, x):
        orig_size = x.shape[2:]
        
        # Backbone
        c1 = self.backbone[0:3](x)  # After 1st stride
        c4 = self.backbone[3:](c1) # After 2nd stride
        
        # ASPP on high-level features
        aspp_out = self.aspp(c4)
        
        # Upsample ASPP output
        aspp_up = F.interpolate(aspp_out, size=c1.shape[2:], mode='bilinear', align_corners=False)
        
        # Get low-level features
        low_level_feat = self.low_level_conv(c1)
        
        # Concatenate and decode
        concat_feat = torch.cat([aspp_up, low_level_feat], dim=1)
        decoder_out = self.decoder(concat_feat)
        
        # Final upsampling
        out = F.interpolate(decoder_out, size=orig_size, mode='bilinear', align_corners=False)
        return out

# --- 3. Core POS + MEO Logic ---

class POS_MEO_Loss(nn.Module):
    """
    Implements the Pareto Optimization Strategy (POS) and
    Magnitude Enhancement Operation (MEO) from the paper.
    """
    def __init__(self, use_meo=True, epsilon=1e-8):
        super().__init__()
        self.use_meo = use_meo
        self.epsilon = epsilon

    def forward(self, model: nn.Module, loss_sup: torch.Tensor, loss_unsup: torch.Tensor):
        params = [p for p in model.parameters() if p.requires_grad]

        # 1. Get gradient vectors g_s and g_u
        g_sup_list = torch.autograd.grad(loss_sup, params, retain_graph=True, create_graph=False)
        g_unsup_list = torch.autograd.grad(loss_unsup, params, retain_graph=True, create_graph=False)

        g_sup_flat = flatten_gradients(g_sup_list)
        g_unsup_flat = flatten_gradients(g_unsup_list)

        # 2. Solve the Pareto Optimization (POS) problem (Eq. 5)
        g_s_minus_g_u = g_sup_flat - g_unsup_flat
        g_s_minus_g_u_norm_sq = torch.dot(g_s_minus_g_u, g_s_minus_g_u) + self.epsilon
        
        alpha_u_opt_unconstrained = torch.dot(g_sup_flat, g_s_minus_g_u) / g_s_minus_g_u_norm_sq

        alpha_u = torch.clamp(alpha_u_opt_unconstrained, 0.0, 1.0)
        alpha_s = 1.0 - alpha_u
        
        alpha_s = alpha_s.detach()
        alpha_u = alpha_u.detach()

        # 3. Calculate the total loss for the *real* backward pass
        total_loss = alpha_s * loss_sup + alpha_u * loss_unsup

        # 4. Calculate the Magnitude Enhancement Operation (MEO) scalar (Eq. 13)
        lambda_val = torch.tensor(1.0, device=total_loss.device)
        if self.use_meo:
            g_pos_flat = alpha_s * g_sup_flat + alpha_u * g_unsup_flat
            g_unif_flat = 0.5 * g_sup_flat + 0.5 * g_unsup_flat

            norm_pos = torch.norm(g_pos_flat)
            norm_unif = torch.norm(g_unif_flat)
            
            lambda_val = norm_unif / (norm_pos + self.epsilon)
            lambda_val = lambda_val.detach()

        return total_loss, lambda_val, alpha_s, alpha_u

# --- 4. Fake Data Generator ---

class FakeSegmentationDataset(data.Dataset):
    """
    Generates fake data to mimic a real segmentation dataset.
    
    Modes:
    - 'labeled': Returns (image, mask)
    - 'unlabeled': Returns (image_weak, image_strong)
    """
    def __init__(self, num_samples, img_size, num_classes, mode='labeled'):
        self.num_samples = num_samples
        self.img_size = img_size
        self.num_classes = num_classes
        self.mode = mode

    def __len__(self):
        return self.num_samples

    def __getitem__(self, idx):
        if self.mode == 'labeled':
            # (img, mask)
            img = torch.randn(3, self.img_size, self.img_size)
            mask = torch.randint(0, self.num_classes, (self.img_size, self.img_size), dtype=torch.long)
            # Add some ignore_index pixels
            if torch.rand(1) > 0.5:
                mask[0:self.img_size//4, 0:self.img_size//4] = IGNORE_INDEX
            return img, mask
        
        elif self.mode == 'unlabeled':
            # (img_weak, img_strong)
            # In a real pipeline, these are two augmentations of the *same* image
            img_weak = torch.randn(3, self.img_size, self.img_size)
            img_strong = img_weak * torch.randn_like(img_weak) + torch.randn_like(img_weak) # Simple strong aug
            return img_weak, img_strong
        
        else:
            raise ValueError(f"Unknown mode: {self.mode}")

# --- 5. Main Training Loop ---

def train():
    """Main training and demonstration function."""
    
    print("--- Full POS+MEO Implementation ---")
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
    print(f"Running on device: {device}")

    # --- Setup Models ---
    student_model = DeepLabv3Plus(num_classes=NUM_CLASSES).to(device)
    teacher_model = DeepLabv3Plus(num_classes=NUM_CLASSES).to(device)
    
    # Initialize teacher with student's weights and stop its gradients
    teacher_model.load_state_dict(student_model.state_dict())
    for param in teacher_model.parameters():
        param.requires_grad = False
    
    print(f"Created Student and Teacher models (DeepLabv3+)")

    # --- Setup DataLoaders ---
    # Create two separate datasets
    labeled_dataset = FakeSegmentationDataset(500, IMG_SIZE, NUM_CLASSES, mode='labeled')
    unlabeled_dataset = FakeSegmentationDataset(2000, IMG_SIZE, NUM_CLASSES, mode='unlabeled')
    
    # Create dataloaders
    labeled_loader = DataLoader(
        labeled_dataset, 
        batch_size=BATCH_SIZE_L, 
        shuffle=True, 
        num_workers=0
    )
    unlabeled_loader = DataLoader(
        unlabeled_dataset,
        batch_size=BATCH_SIZE_U,
        shuffle=True,
        num_workers=0
    )
    
    # Iterators for the training loop
    labeled_iter = iter(labeled_loader)
    unlabeled_iter = iter(unlabeled_loader)
    
    print(f"Created FakeDataLoaders: {len(labeled_dataset)} labeled, {len(unlabeled_dataset)} unlabeled.")

    # --- Setup Optimizer and Loss ---
    optimizer = optim.Adam(student_model.parameters(), lr=LEARNING_RATE)
    
    # Standard Cross-Entropy for pixel-wise loss
    ce_loss_fn = nn.CrossEntropyLoss(ignore_index=IGNORE_INDEX)
    
    # Our custom POS+MEO loss wrapper
    pos_meo_criterion = POS_MEO_Loss(use_meo=True).to(device)
    
    # --- Training Epochs ---
    for epoch in range(EPOCHS):
        print(f"\n--- Epoch {epoch+1}/{EPOCHS} ---")
        student_model.train()
        
        for step in range(STEPS_PER_EPOCH):
            # --- Get Data Batches ---
            try:
                labeled_img, labeled_mask = next(labeled_iter)
            except StopIteration:
                labeled_iter = iter(labeled_loader)
                labeled_img, labeled_mask = next(labeled_iter)
            
            try:
                unlabeled_weak, unlabeled_strong = next(unlabeled_iter)
            except StopIteration:
                unlabeled_iter = iter(unlabeled_loader)
                unlabeled_weak, unlabeled_strong = next(unlabeled_iter)
                
            labeled_img, labeled_mask = labeled_img.to(device), labeled_mask.to(device)
            unlabeled_weak, unlabeled_strong = unlabeled_weak.to(device), unlabeled_strong.to(device)

            # --- 1. Supervised Loss ---
            labeled_preds = student_model(labeled_img)
            loss_sup = ce_loss_fn(labeled_preds, labeled_mask)

            # --- 2. Unsupervised Loss ---
            # Generate pseudo-labels with teacher (no gradients)
            with torch.no_grad():
                teacher_preds_weak = teacher_model(unlabeled_weak)
                
                # Get confidence and pseudo-labels (Eq. 2)
                probs = F.softmax(teacher_preds_weak, dim=1)
                confidence, pseudo_labels = torch.max(probs, dim=1)
                
                # Apply confidence threshold
                mask_confidence = confidence > CONFIDENCE_THRESHOLD
                pseudo_labels[~mask_confidence] = IGNORE_INDEX

            # Calculate student loss on strong augmentations
            student_preds_strong = student_model(unlabeled_strong)
            loss_unsup = ce_loss_fn(student_preds_strong, pseudo_labels)

            # --- 3. Apply POS and MEO ---
            # This is the core logic from the paper.
            # We get the combined loss and the MEO scalar.
            total_loss, lambda_val, alpha_s, alpha_u = pos_meo_criterion(
                student_model, loss_sup, loss_unsup
            )
            
            # --- 4. Optimization ---
            optimizer.zero_grad()
            
            # Backward pass on the POS-weighted loss
            total_loss.backward()

            # Apply MEO Gradient Scaling (Eq. 13)
            if pos_meo_criterion.use_meo and lambda_val != 1.0:
                with torch.no_grad():
                    for param in student_model.parameters():
                        if param.grad is not None:
                            param.grad.data.mul_(lambda_val)
            
            optimizer.step()
            
            # --- 5. Update Teacher Model ---
            update_teacher_model(student_model, teacher_model, EMA_ALPHA)

            # --- Logging ---
            if (step + 1) % 10 == 0:
                print(f"  Step {step+1}/{STEPS_PER_EPOCH} | "
                      f"L_sup: {loss_sup.item():.4f} (w: {alpha_s.item():.2f}) | "
                      f"L_unsup: {loss_unsup.item():.4f} (w: {alpha_u.item():.2f}) | "
                      f"MEO (λ): {lambda_val.item():.3f}")

    print("\n--- Training Complete ---")

if __name__ == "__main__":
    # Note: This will be slow if not run on a GPU.
    train()

Related posts, You May like to read