5 Revolutionary Advancements in Medical Image Segmentation: How SDCL Outperforms Existing Methods (With Math Explained)

Introduction: The Evolution of Medical Image Segmentation

Medical image segmentation plays a pivotal role in diagnostics, treatment planning, and clinical research. As technology advances, the demand for accurate, efficient, and scalable segmentation methods has never been higher. However, the field faces a significant challenge: limited labeled data . Annotating medical images is time-consuming, expensive, and requires expert knowledge.

This is where semi-supervised learning (SSL) comes into play. By leveraging both labeled and unlabeled data , SSL methods aim to bridge the gap between limited supervision and high performance. One of the most promising innovations in this space is SDCL (Students Discrepancy-Informed Correction Learning) — a novel framework that redefines how we approach medical image segmentation by addressing the confirmation and cognitive biases that plague traditional teacher-student models.

In this article, we’ll explore how SDCL works, its advantages over existing methods, and the mathematical foundation that powers its superior performance. Whether you’re a researcher, developer, or healthcare professional, this guide will provide valuable insights into the future of medical imaging.

What is SDCL? A Game-Changer in Semi-Supervised Medical Image Segmentation

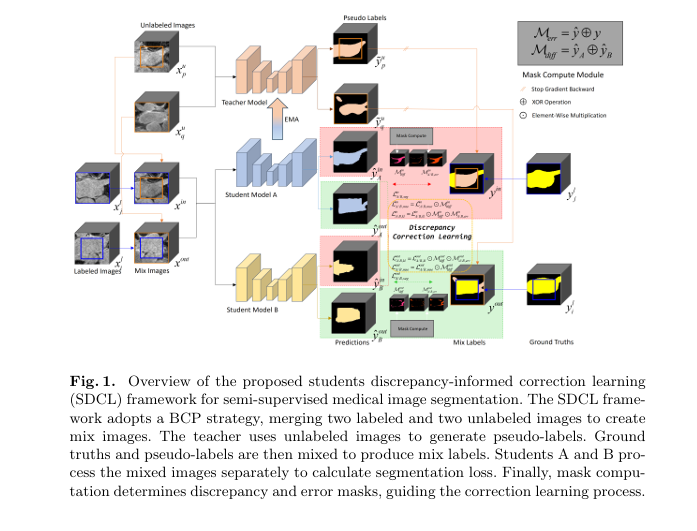
Understanding the SDCL Framework

SDCL introduces a three-model architecture consisting of:

Two structurally different students (Student A and Student B)
One non-trainable teacher (based on Exponential Moving Average or EMA)

Unlike traditional Mean Teacher (MT) frameworks that rely on a single student model, SDCL leverages discrepancy maps generated by comparing the outputs of two diverse students. These maps highlight areas of segmentation disagreement , which are then used to guide correction learning .

Why It Matters

Diversity and Stability : Using two different student models (e.g., VNet and ResVNet for 3D tasks) ensures diverse predictions, reducing overfitting and increasing robustness.
Bias Correction : SDCL actively identifies and corrects confirmation and cognitive biases in pseudo-labels.
Performance : SDCL achieves state-of-the-art (SOTA) results , outperforming existing methods by 2.57% to 3.04% in Dice score across three major datasets.

The Problem with Traditional Teacher-Student Models

Before diving into SDCL’s innovation, let’s understand the limitations of traditional SSL methods in medical image segmentation:

1. Confirmation Bias

When a model generates pseudo-labels from its own predictions, it tends to reinforce its own mistakes .
This leads to confirmation bias , where incorrect labels are treated as ground truth.

2. Cognitive Bias

Models may misinterpret ambiguous regions , especially in complex medical images like MRI or CT scans.
Without diverse perspectives, these biases go uncorrected.

3. Single Model Limitation

Most SSL frameworks use one student model , which limits the diversity of pseudo-labels.
This results in suboptimal performance and reduced generalization .

How SDCL Solves These Problems

1. Dual Student Architecture

SDCL introduces two trainable students with different architectures :

3D Tasks : VNet (Student A) and ResVNet (Student B)
2D Tasks : U-Net (Student A) and ResU-Net (Student B)

This diversity ensures that the model sees the data from different perspectives , reducing the risk of confirmation bias.

2. Discrepancy Mask (Mdiff)

\[ M_{\text{diff}}^{\text{in/out}} = \tilde{y}_{\text{in/out}}^A \oplus \tilde{y}_{\text{in/out}}^B \]

Where:

y is the argmax of the predicted segmentation
⊕ denotes the XOR operation

This mask highlights regions where the two students disagree , signaling potential bias areas .

3. Error Mask (Merr)

To further refine the correction process, SDCL generates an error mask Merr by comparing student predictions with the mix labels :

\[ M_{\text{err}}^{\text{in/out}} = \tilde{y}_{\text{in/out}}^{A/B} \oplus y_{\text{in/out}} \]

This mask identifies regions where the student’s prediction differs from the teacher’s pseudo-label , indicating potential errors .

4. DiffErr Mask (Mdifferr)

Finally, SDCL combines the two masks to create a DiffErr mask :

\[ M_{\text{differr}}^{\text{in/out}} = M_{\text{err}}^{\text{in/out}} \cdot M_{\text{diff}}^{\text{in/out}} \]

This final mask is used to guide the correction learning process , focusing on both discrepancy and error regions .

The Correction Learning Process

SDCL employs two loss functions to guide the model in correcting its biases:

1. Mean Squared Error (MSE) Loss

The MSE loss minimizes the distance between correct predictions in discrepancy regions:

\[ \mathcal{L}_{\text{mse}}^{\text{in/out}} = \mathcal{L}_{\text{mse}}(\hat{y}_{\text{in/out}}^{A/B}, y_{\text{in/out}}) \cdot M_{\text{diff}}^{\text{in/out}} \]

This encourages the model to review and reinforce correct cognition in areas of disagreement.

2. Kullback-Leibler (KL) Divergence Loss

The KL divergence loss maximizes the entropy of erroneous predictions , effectively resetting misclassified regions to a uniform distribution:

\[ \mathcal{L}_{\text{kl}}^{\text{in/out}} = D_{\text{KL}}(u \parallel \hat{y}_{\text{in/out}}^{A/B}) \cdot M_{\text{differr}}^{\text{in/out}} \]

Where:

u is the uniform distribution
y is the model’s output

This loss helps the model self-correct errors in uncertain regions.

Performance Evaluation: SDCL vs. State-of-the-Art Methods

Dataset Overview

SDCL was evaluated on three public medical image datasets :

DATASET	MODALITY	LABELED	UNLABELED	TASK
Pancreas-NIH	CT	12	50	Organ segmentation
LA (Left Atrium)	MRI	8	72	Cardiac segmentation
ACDC	MRI	7	63	Cardiac segmentation

Results

Pancreas-CT Dataset

METHOD	DICE	JAC	95HD	ASD
V-Net	70.59	56.77	14.19	2.25
BCP	82.91	70.97	6.43	2.25
SDCL (Ours)	85.04	74.22	5.22	1.48

Left Atrium (LA) Dataset

METHOD	DICE	JAC	95HD	ASD
U-Net	79.87	67.60	26.65	7.94
BCP	89.62	81.31	6.81	1.76
SDCL (Ours)	92.35	85.83	4.22	1.44

ACDC Dataset

METHOD	DICE	JAC	95HD	ASD
U-Net	79.41	68.11	9.35	2.70
BCP	88.84	80.62	3.98	1.17
SDCL (Ours)	90.92	83.83	1.29	0.34

Key Takeaways

SDCL outperforms BCP by 2.13% to 3.04% in Dice score.
On the ACDC dataset , SDCL surpasses the fully supervised method .
The ASD metric shows a 39% reduction in surface distance compared to U-Net.

Ablation Study: Understanding the Impact of Each Component

COMPONENT	DICE	JAC	95HD	ASD
Baseline (Lseg only)	83.23	71.57	8.53	2.49
+ Lmse	83.67	72.20	9.12	2.80
+ Lkl	84.20	73.01	6.25	2.03
+ Mdiff	85.04	74.23	5.22	1.48

Insights

Mdiff contributes the most to performance improvement (+1.17% Dice).
Combining Lmse and Lkl further enhances accuracy.
Full SDCL achieves a 2.16% improvement over baseline.

If you’re Interested in Directed Graph Learning using deep learning, you may also find this article helpful: 9 Explosive Strategies & Hidden Pitfalls in Data-Centric Directed Graph Learning

Real-World Applications and Future Directions

Clinical Impact

Improved diagnosis accuracy in cardiac and pancreatic imaging.
Faster treatment planning through automated segmentation.
Reduced workload for radiologists and clinicians.

Research Opportunities

Refining the teacher model using student feedback.
Extending SDCL to multi-modal and 4D medical imaging .
Exploring domain adaptation for cross-dataset generalization.

Conclusion: SDCL — The Future of Medical Image Segmentation

SDCL represents a paradigm shift in semi-supervised medical image segmentation. By addressing the confirmation and cognitive biases inherent in traditional SSL frameworks, it delivers superior performance with minimal labeled data .

Whether you’re developing AI-driven diagnostic tools or researching new segmentation techniques, SDCL offers a robust, scalable, and mathematically sound solution.

Call to Action

Ready to take your medical image segmentation projects to the next level?
👉 Download the SDCL source code on GitHub and start experimenting today!
🔗 SDCL GitHub Repository

If you found this article helpful, share it with your colleagues or leave a comment below!
Have questions about SDCL or semi-supervised learning? Ask away — we’re here to help.

Here, implementation of the proposed SDCL framework using Pytorch:

import torch
import torch.nn.functional as F
import torch.nn as nn

# -----------------------------------------------------------
# 1. Student Models: Choose different architectures
# -----------------------------------------------------------

class DoubleConv(nn.Module):
    def __init__(self, in_channels, out_channels):
        super().__init__()
        self.unit = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, 3, padding=1),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(inplace=True),
            nn.Conv2d(out_channels, out_channels, 3, padding=1),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(inplace=True)
        )

    def forward(self, x):
        return self.unit(x)

class StudentA_UNet(nn.Module):
    def __init__(self, in_channels=1, num_classes=2):
        super().__init__()
        self.down1 = DoubleConv(in_channels, 64)
        self.pool1 = nn.MaxPool2d(2)
        self.down2 = DoubleConv(64, 128)
        self.pool2 = nn.MaxPool2d(2)
        self.down3 = DoubleConv(128, 256)
        self.pool3 = nn.MaxPool2d(2)
        self.bottom = DoubleConv(256, 512)
        self.up3 = nn.ConvTranspose2d(512, 256, 2, stride=2)
        self.dec3 = DoubleConv(512, 256)
        self.up2 = nn.ConvTranspose2d(256, 128, 2, stride=2)
        self.dec2 = DoubleConv(256, 128)
        self.up1 = nn.ConvTranspose2d(128, 64, 2, stride=2)
        self.dec1 = DoubleConv(128, 64)
        self.out_conv = nn.Conv2d(64, num_classes, kernel_size=1)

    def forward(self, x):
        enc1 = self.down1(x)
        enc2 = self.down2(self.pool1(enc1))
        enc3 = self.down3(self.pool2(enc2))
        bottleneck = self.bottom(self.pool3(enc3))
        dec3 = self.dec3(torch.cat([self.up3(bottleneck), enc3], dim=1))
        dec2 = self.dec2(torch.cat([self.up2(dec3), enc2], dim=1))
        dec1 = self.dec1(torch.cat([self.up1(dec2), enc1], dim=1))
        return self.out_conv(dec1)




class ResidualBlock(nn.Module):
    def __init__(self, channels):
        super().__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(channels, channels, 3, padding=1),
            nn.BatchNorm2d(channels),
            nn.ReLU(inplace=True),
            nn.Conv2d(channels, channels, 3, padding=1),
            nn.BatchNorm2d(channels)
        )
        self.relu = nn.ReLU(inplace=True)

    def forward(self, x):
        return self.relu(x + self.conv(x))

class StudentB_ResUNet(nn.Module):
    def __init__(self, in_channels=1, num_classes=2):
        super().__init__()
        self.down1 = ResidualBlock(in_channels)
        self.pool1 = nn.MaxPool2d(2)
        self.down2 = ResidualBlock(in_channels)
        self.pool2 = nn.MaxPool2d(2)
        self.down3 = ResidualBlock(in_channels)
        self.pool3 = nn.MaxPool2d(2)
        self.bottom = ResidualBlock(in_channels)
        self.up3 = nn.ConvTranspose2d(in_channels, in_channels, 2, stride=2)
        self.dec3 = ResidualBlock(in_channels)
        self.up2 = nn.ConvTranspose2d(in_channels, in_channels, 2, stride=2)
        self.dec2 = ResidualBlock(in_channels)
        self.up1 = nn.ConvTranspose2d(in_channels, in_channels, 2, stride=2)
        self.dec1 = ResidualBlock(in_channels)
        self.out_conv = nn.Conv2d(in_channels, num_classes, kernel_size=1)

    def forward(self, x):
        enc1 = self.down1(x)
        enc2 = self.down2(self.pool1(enc1))
        enc3 = self.down3(self.pool2(enc2))
        bottleneck = self.bottom(self.pool3(enc3))
        dec3 = self.dec3(self.up3(bottleneck) + enc3)
        dec2 = self.dec2(self.up2(dec3) + enc2)
        dec1 = self.dec1(self.up1(dec2) + enc1)
        return self.out_conv(dec1)

# -----------------------------------------------------------
# 2. Teacher Model (EMA version of StudentA)
# -----------------------------------------------------------

class EMA:
    def __init__(self, model, decay=0.99):
        self.shadow = {name: param.clone() for name, param in model.named_parameters()}
        self.decay = decay

    def update(self, model):
        with torch.no_grad():
            for name, param in model.named_parameters():
                self.shadow[name].data.mul_(self.decay).add_((1 - self.decay) * param.data)

    def apply_to(self, model):
        for name, param in model.named_parameters():
            param.data.copy_(self.shadow[name].data)

# -----------------------------------------------------------
# 3. Mix Image and Label Generator (BCP Strategy)
# -----------------------------------------------------------

def mix_images(x_a, x_b, mask):
    return x_a * mask + x_b * (1 - mask)

def mix_labels(y_a, y_b, mask):
    return y_a * mask + y_b * (1 - mask)

# -----------------------------------------------------------
# 4. Discrepancy Masks
# -----------------------------------------------------------

def compute_diff_mask(pred_a, pred_b):
    """
    XOR mask between two student predictions
    """
    return torch.abs(torch.argmax(pred_a, dim=1) - torch.argmax(pred_b, dim=1)) > 0

def compute_error_mask(pred, label):
    """
    Mask where prediction mismatches ground truth
    """
    return torch.argmax(pred, dim=1) != torch.argmax(label, dim=1)

def compute_diff_error_mask(diff_mask, err_mask):
    return diff_mask & err_mask

# -----------------------------------------------------------
# 5. Loss Functions: Correction Learning
# -----------------------------------------------------------

def mse_loss(pred, label, mask):
    loss = F.mse_loss(pred, label, reduction='none')
    return torch.mean(loss[mask])

def kl_divergence(pred, num_classes, mask):
    # Pull prediction towards uniform distribution
    u = torch.full_like(pred, 1.0 / num_classes)
    loss = F.kl_div(F.log_softmax(pred, dim=1), u, reduction='none')
    return torch.mean(loss[mask])

# -----------------------------------------------------------
# 6. Total Loss Composition
# -----------------------------------------------------------

def total_loss(pred_a, pred_b, mix_label, mse_mask, kl_mask, alpha=0.5, gamma=0.3, delta=0.1):
    # Segmentation loss
    seg_loss = F.cross_entropy(pred_a, torch.argmax(mix_label, dim=1)) + \
               F.cross_entropy(pred_b, torch.argmax(mix_label, dim=1))

    # Correction learning losses
    mse = mse_loss(pred_a, mix_label, mse_mask) + mse_loss(pred_b, mix_label, mse_mask)
    kl  = kl_divergence(pred_a, mix_label.shape[1], kl_mask) + kl_divergence(pred_b, mix_label.shape[1], kl_mask)

    return seg_loss + gamma * mse + delta * kl

# -----------------------------------------------------------
# 7. Training Step
# -----------------------------------------------------------

def training_step(student_a, student_b, teacher, optimizer, x_labeled, y_labeled, x_unlabeled, mask):
    # Generate mix images/labels
    x_mixed = mix_images(x_labeled, x_unlabeled, mask)
    y_mixed = mix_labels(y_labeled, teacher(x_unlabeled), mask)

    # Forward pass
    out_a = student_a(x_mixed)
    out_b = student_b(x_mixed)

    # Update EMA teacher
    teacher.update(student_a)

    # Compute discrepancy masks
    diff_mask = compute_diff_mask(out_a, out_b)
    error_mask = compute_error_mask(out_a, y_mixed)
    kl_mask = compute_diff_error_mask(diff_mask, error_mask)

    # Total loss
    loss = total_loss(out_a, out_b, y_mixed, diff_mask, kl_mask)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()